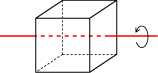
A symmetry of a polyhedron is a way of moving the polyhedron so that it occupies the same physical space as before it was moved. As an example, consider the symmetries of the cube. A cube can be rotated 90°, 180°, or 270° around an axis passing through the centers of two opposite faces of the cube,
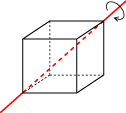
or it can be rotated 120° or 240° around an axis passing through two opposite vertices of the cube,
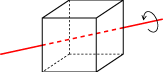
or it can be rotated 180° around an axis passing through the midpoints of two opposite edges of the cube.
In fact, these comprise all of the symmetries of the cube except for the mundane but mathematically important move of leaving the cube where it is.
The symmetries of a polyhedron reflect its structure and regularity. A polyhedron is regular if there is a symmetry taking any face to any other face and a symmetry taking any vertex to any other vertex, and a polyhedron with regular faces is semi-regular if there is a symmetry taking any vertex to any other vertex.
Other types of geometric figures also have symmetries. To play around with symmetries in the plane, check out the University of Minnesota Geometry Center program Kali, which lets you make patterns that correspond to each of the 17 wallpaper groups.
A permutation is a way of rearranging a finite set of objects. For instance, we can define a permutation σ of four objects by
 BCAD,
BCAD, meaning that σ puts the first letter into the third position, puts the second letter into the first position, puts the third letter into the second position, and leaves the fourth letter fixed.
If we have two permutations of the same number of objects, we can combine them to form a third permutation. Taking the permutation
 BADC,
BADC, which swaps the first and second letters and swaps the third and fourth letters, and the permutation σ above, we can create a new permutation, which we will denote σ * σ, by performing σ and then τ. That is,
 BCAD
BCAD  CBDA.
CBDA. The permutations of a fixed number of objects together with the operation * have the mathematical structure of a group. Below are enumerated the properties that make the permutations into a group; offered for comparison are the corresponding properties of the more familiar group of real numbers with the operation +.
| Associativity | |
|---|---|
| (α * β) * γ = α * β * γ) | (a + b) + c = a + (b + c) |
| Identity | |
| The identity is the permutation ε
which moves nothing: ε * α = α * ε = α |
The identity is 0: a + 0 = 0 + a = a |
| Inverses | |
| Every permutation α has an
inverse
permutation β, obtained by reversing all of the moves of α, such that α * β = β * α = ε (For example, the inverse of τ
above
is τ, |
Every number a has an additive inverse -a, such that a + (-a) = (-a) + a = 0 |
A major difference between a group of permutations and the additive group of numbers is that while the latter is commutative, i.e., a + b = b + a, the former is usually not:
 BADC
BADC  ADBC,
ADBC, which is not the same as σ * τ.
The group of all permutations of a set of n objects is called the symmetric (permutation) group on n letters, denoted Sn. There is a smaller group contained in Sn called the alternating (permutation) group on n letters, denoted An, which consists of only the even permutations.
A permutation is called even if it can be acheived by swapping pairs of objects an even number of times. For instance,
 CAB
CAB is even because it is obtained by swapping the first and second letters and then the first and third letters, while
 BAC
BAC is not even. It turns out that exactly half of the permutations in any given Sn are even.
The models above are colored to show an equivalence between the symmetry groups of the regular polyhedra and certain permutation groups. In each case, the symmetries of the polyhedron correspond to either all permutations of the colors or the even permutations of the colors, as follows.
| Polyhedron | Symmetry Group |
|---|---|
| Tetrahedron | A4 |
| Cube | S4 |
| Octahedron | |
| Dodecahedron | A5 |
| Icosahedron |
Remark: Opposite corners of the cube below (and opposite faces of the octahedron below) have the same color.

Consider as an example the model cube, in which the white portions should not be counted as a color for these purposes. The permutation
 GRBY
GRBY corresponds to a rotation by 90° around an axis passing through the centers of the front and back faces, the permutation
 RYGB
RYGB corresponds to a rotation around an axis passing through the red vertices, and the permutation
 GBYR
GBYR corresponds to a rotation around an axis passing through the two red-green edges. That the symmetry group of the cube is S4 means that any permutation of the colors can be achieved by some symmetry of the cube and vice versa.
Remark: The twisted dodecahedron model in the photo above, made with Thomas Hull's PHiZZ Unit, has been replaced by the more accurate dodecahedron model pictured below, made with an ancestor of the PHiZZ Unit that was developed by Robert Neale. The folding pattern is similar to that of the PHiZZ Unit and experienced folders should have little trouble reproducing it.
