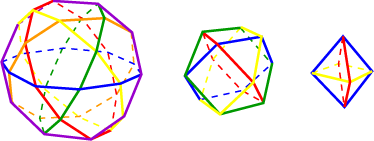
What the Origami Means, Part II
Dual Polyhedra


Remark: Since I am not expert in devising original origami forms, I generally assemble origami modules invented by other people into mathematical models that interest me. There are only two bits of paper folding in this display for which I can even remotely take credit, and both are pictured above. First, I made the straightforward discovery that Tomoko Fuse's Plain Open Frame Unit (the most prevalent module in the display) can be assembled with some of its creases reversed to form support struts for pentagonal faces (notice the yellow struts in the largest model above). This method remains the best technique I know for modeling solids that contain pentagonal and triangular faces. Second, for the intersecting dual pair models in the back row, I had to develop the yellow dodecahedron-corner inserts to complete the set, which otherwise consists of units from Tomoko Fuse's arsenal. The inserts use a trigonometric approximation which I later discovered to be related to the approximation used in the dodecahedron units shown below.
The centers of the faces of any regular polyhedron form the vertices of another regular polyhedron. For example, if we take the centers of the faces of a cube and connect them with edges and faces, we obtain an octahedron. For this reason, the octahedron is called the dual of the cube.
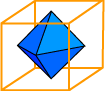
In fact, the reverse is also true; if we take the centers of the faces of an octahedron and connect them with edges and faces, we get a cube.
In the same fashion, the icosahedron and dodecahedron are duals, and the tetrahedron is its own dual.
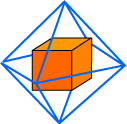
Returning to the octahedron inscribed in the cube, we can imagine
gradually enlarging the octahedron until its edges just touch the
edges of the cube. (Of course, the same can be done with the cube
inside the octahedron.) The resulting figure, pictured below, is
one of the three intersecting-dual-pair models above.
[Back row, left to right:
Icosahedron/Dodecahedron, Octahedron/Cube, Tetrahedron/Tetrahedron]
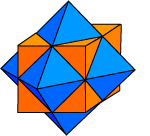
By taking the dual-pair solids and chopping
off
all of the pyramidal
protrusions, we obtain the icosidodecahedron, the cuboctahedron,
and the octahedron, semi-regular solids which contain all of the
faces of two dual Platonic solids. Alternately, each figure can be
obtained in two ways (one, in the octahedron's case) by truncating
a single regular solid. The cuboctahedron can be formed either by
slicing the corners off of a cube to create the eight triangles of
an octahedron or by slicing the corners off of an octahedron to
create the six squares of a cube.
[Front row, left to right:
Icosidodecahedron, Cuboctahedron, "Tetratetrahedron" (Octahedron)]

The icosidodecahedron, the cuboctahedron, and the "tetratetrahedron" have duals of their own. The geometry of the Zometool construction system makes it straightforward to construct models of these Archimedean duals.
The edges of an icosidodecahedron form six regular decagons, each of which bisects the icosidodecahedron. This is one reason that collapsible Hoberman Spheres can easily be constructed as icosidodecahedral linkages. Similarly, the edges of a cuboctahedron form four regular hexagons, and the edges of an octahedron form three squares.