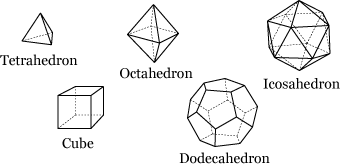
There are only five regular solids, all of which are pictured
below.
The Greek names of the solids refer to the number
of faces they have: "tetra-" means four, "octa-" means eight,
"dodeca-" means twelve, and "icosa-" means twenty.

A semi-regular or Archimedean solid is characterized by the following properties:
Clearly, each of the regular solids is also semi-regular, but there are many additional solids that meet these looser conditions. Most of them are closely related to the regular solids and can be constructed by cutting, combining, or distorting their Platonic relatives. Many of these hybrid solids are modeled in this display.


Remark: The
photograph above was taken eight years
after the display was installed. The rhombicosadodecahedron
model, whose unsupported pentagons make it the least stable of the
hanging models, has sagged considerably over the years.
The truncated polyhedra are formed by slicing the corners off of
the tetrahedron, the octahedron, and the icosahedron. In each
case, the triangular faces of the original solid become hexagons.
Notice that the truncated icosahedron is the pattern of stitches
on a soccerball.
To form a rhombicuboctahedron, imagine taking a cube and pulling its six square faces away from each other as though the edges of the cube were made of elastic. Each edge of the cube turns into another square, and each vertex turns into a triangle, and the resulting solid is the rhombicuboctahedron. The same solid results if the faces of an octahedron are pulled apart; to understand why, see the description of dual polyhedra below. A similar relationship connects the rhombicosidodecahedron to a dodecahedron or an icosahedron. Pulling apart the triangular faces of a tetrahedron yields the cuboctahedron, further described below.
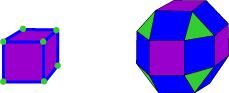
I have devised a Zometool model of the rhombicosidodecahedron which illustrates its relationship to the icosahedron and the dodecahedron.
Now, once again imagine pulling apart the faces of a cube, and imagine that the original square faces of the cube and the triangles that were once the vertices of the cube are rigid like pieces of metal and are joined at the corners. If the rigid squares are simultaneously twisted in just the right way, the former edges of the cube will collapse from squares into pairs of equilateral triangles, and the new solid will be a snub cube. The other snub solids arise in a similar fashion.

Here is another set of snub solid models which is colored differently than but otherwise identical to the one in the Amherst display. This one lives by my office.
