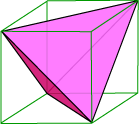
We can use a similar construction to relate the symmetry groups of the tetrahedron and of the cube. As shown below, it is possible to inscribe a tetrahedron in a cube in such a way that the vertices of the tetrahedron are four of the eight vertices of the cube.

The other four vertices of the cube form the vertices of another tetrahedron; this can be seen by looking at the model of two intersecting tetrahedra among the dual polyhedra models above, in which the edges of the two tetrahedra are the diagonals of the square faces of the circumscribed cube. It is clear that every symmetry of the cube will either cause both tetrahedra to occupy the same space as before or exchange the positions of the two tetrahedra. What is not as clear but equally true is that it is precisely the symmetries of the cube leaving the two tetrahedra unswapped (namely the identity, rotations through pairs of opposite vertices, and rotations by 180° through centers of opposite faces) that correspond to the even permutations in S4. In other words, the symmetries of each tetrahedron sitting in the cube correspond to the permutation group A4 contained in S4.


The model above, made after the Amherst installation, further illustrates the relationships between the cube, the octahedron, and the tetrahedron. It consists of four copies of a simple origami octahedron (if you know any origami, try your hand at making such an octahedron by fitting together six waterbomb bases), connected with a simple linkage. The resulting figure fits naturally inside a tetrahedron: in fact, its convex hull (think of this as the shape you would get if you wrapped the model in plastic wrap) is a truncated tetrahedron. The origami form can be viewed as six intersecting rectangles, each of which is a doubled square. Although it is difficult to see in these photographs, the solid bounded by these six rectangles is a cube. One vertex of the cube is resting on the ground and the opposite vertex is in the center of the top triangle in the left picture. Four of the eight vertices of this central cube are the centers of the four octahedra and form the vertices of a tetrahedron parallel to the tetrahedron circumscribing the model.
Three-dimensional space can be tiled by octahedra and tetrahedra with a fixed edge length; in the tiling, each triangular face has an octahedron on one side and a tetrahedron on the other. The model above this text represents a tetrahedron surrounded by four octahedra within this tiling. Adding ten more tetrahedra yields the larger tetrahedron described above. In a similar vein, the intersecting dual tetrahedra model can also be viewed as an octahedron surrounded by eight tetrahedra and may be interspersed with octahedra to fill space.
As a corollary to the embedding of a tetrahedron in a cube, it is also possible to find five cubes in a dodecahedron that are permuted by the symmetries of the dodecahedron. The edges of these cubes are the sixty diagonals of the pentagonal faces of the dodecahedron. Below are pictures of the model in the lower right corner of the Amherst origami display, which shows the cubes through a combination of paper and thread. My thanks go to Irene Starr for these photographs.
 |
 |
Furthermore, it is possible to inscribe an octahedron in a tetrahedron (in fact, if you stellate an octahedron, you get the intersecting tetrahedra modeled above) and to inscribe an icosahedron in an octahedron. If you combine all of these constructions, you get a nifty nesting of all five regular solids. Here are two non-origami models of this arrangement.
 |
 |
Drinking Straws |
Zometool |
Zometool now has a package called Kepler's Obsession, which contains all the parts you need to make the model above but with different colors for each regular solid. If you are a Zometool enthusiast, you may want to make this investment; even if you do not mind the poor coloring of the model above, you need some of the rarer lengths of green edges to complete it.