Geometric Conundrum

[Integers] [Rationals] [Square Roots] [Regular Polygons]

Pose these questions to your Geometry class:

Using a straight-edge and a compass,

Can you construct the set of Integers starting with the unit 1? How?

Start be constructing a segment with a straight-edge. Call its length, 1. Now copy this length onto the end of the original segment. You have constructed length 2.

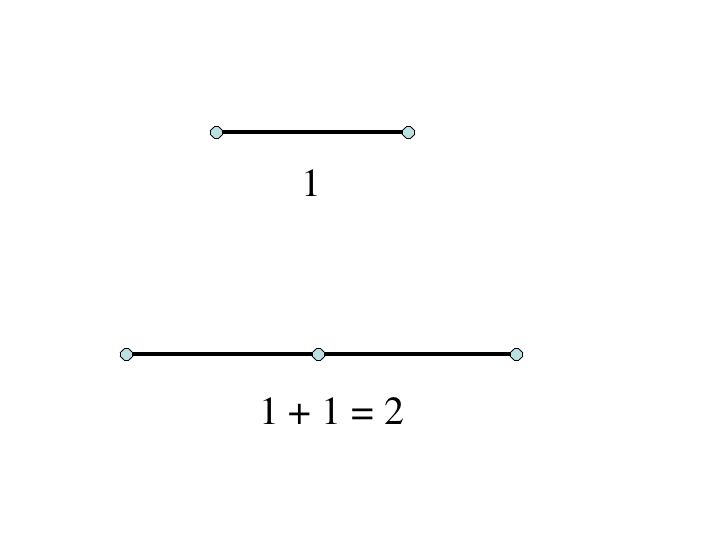
Copy the original length 1 onto length 2 and you have constructed the length 3.

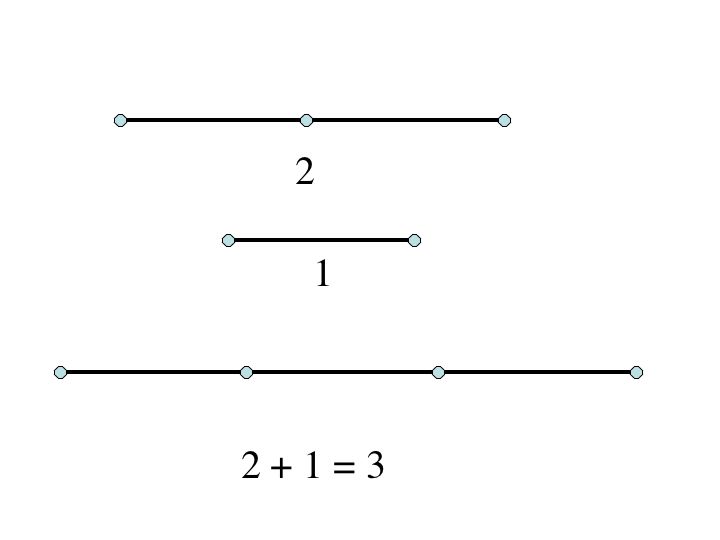
Continue to repeat this process and you will construct all the positive integers. To get the negative integers we work backwards and take away 1 unit. So if we start with length 3 and take away length 1, we are left with a legth of 2. Thus we have constructed -1.

[TOP]

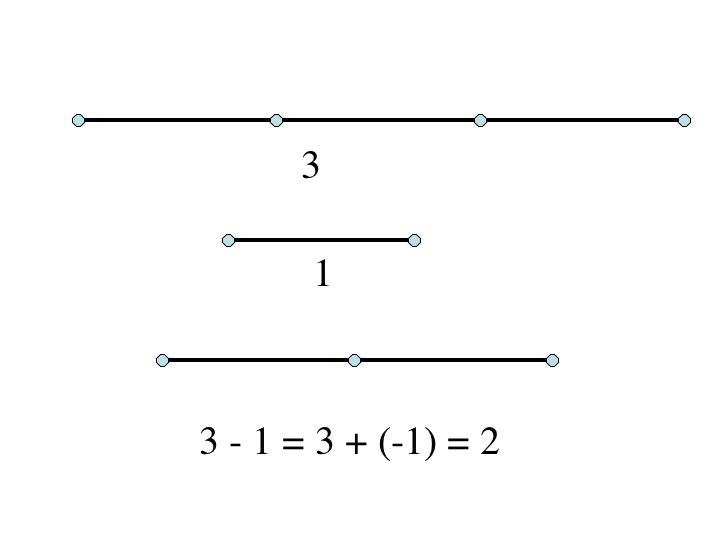
Can you construct the set of Rational numbers starting with the unit 1? How?

From the constructible lengths section, we already know how to construct 1/2 when starting with length 1. We take a segment and draw the perpendicular bisector to the segment using a compass and straight-edge. Starting with length 1, lets construct length 1/3.

Start by constructing a segment with a straight-edge. Call its length, 1.

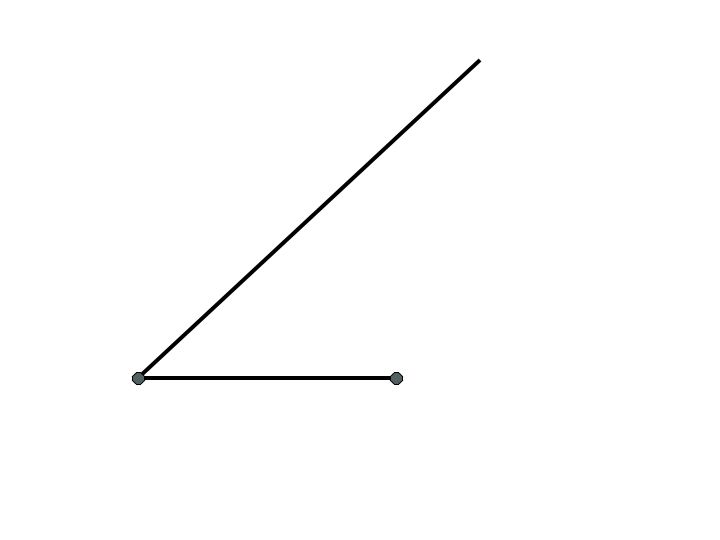
Using a straight-edge, construct a ray from one endpoint of the original segment.

Choose a length n. Starting at the intersecting point of the segment and the ray, mark off length n on the ray. Then starting at the new mark on the ray, measure and mark another length n, and then again. You have now broken the ray up into 3 equal segments and a remaining length that we will ignore for now.

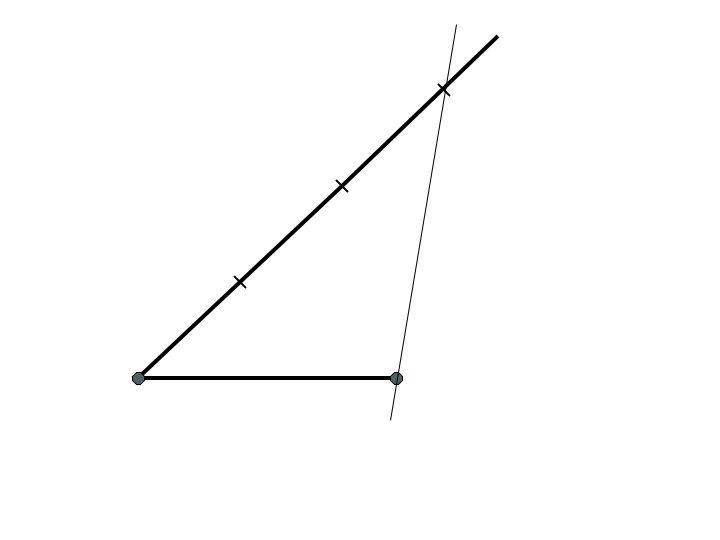
Using a straight-edge, construct a line intersecting the third mark on the ray and the endpoint of the segment. Call that line l.

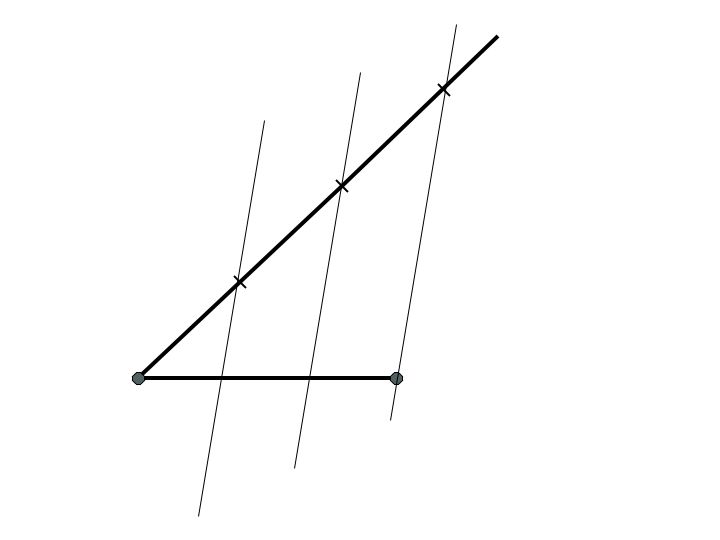
Now construct two more lines, one line, m, parallel to line l, intersecting the second mark and the other line, n, parallel the line l, intersection the first mark. All three of these lines are parallel to each other. The length from the vertex to the intersection point between line n and the original segment, on the original segment, is 1/3. The length from the vertex to the intersection point between line m and the original segment, on the original segment, is 2/3.

We have just constructed lengths 1/3 and 2/3. We can use a similar process to construct the rest of the rational numbers. Instead of marking off 3 congruent lengths on the ray, mark of 5 congruent lengths, and you can construct 1/5, 2/5, 3/5, and 4/5. Now you can mark off 4 congruent lengths so that you can construct 1/4, 2/4, or 3/4 but all of these can be constructed more easily by constructing perpendicular bisectors of a segment. First, construct the perpendicular bisector of a segment with length 1. This will give you a segment with length 1/2. Now construct the perpendicular bisector of this segment and you will construct a length of 1/4. We already know we can add lengths, so we can construct 3/4 by adding 1/4 + 1/2. Using this process we can construct any rational number with an even denominator. For all other rational numbers, use the process outlined in the paragraph before.

[TOP]

Can you construct the square root of any natural number starting with the unit 1? How?

Start be constructing a segment with a straight-edge. Call its length, 1.

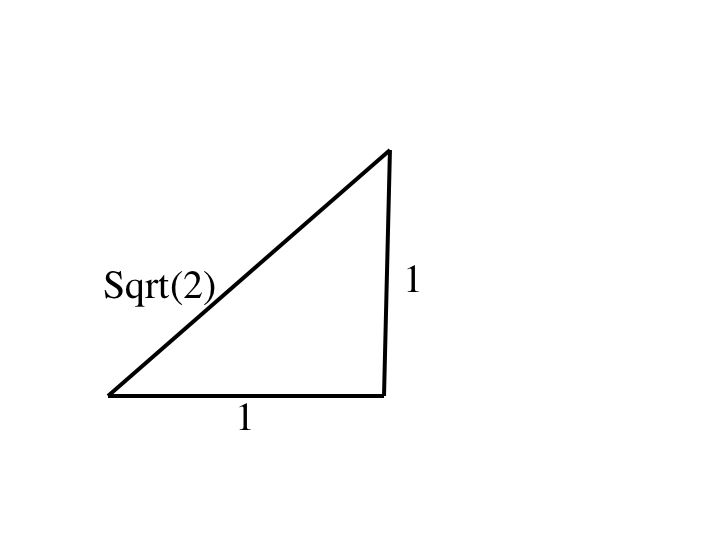
Construct a 45-45-90 triangle, with both legs having length 1 and hypothenuse length sqrt(2).

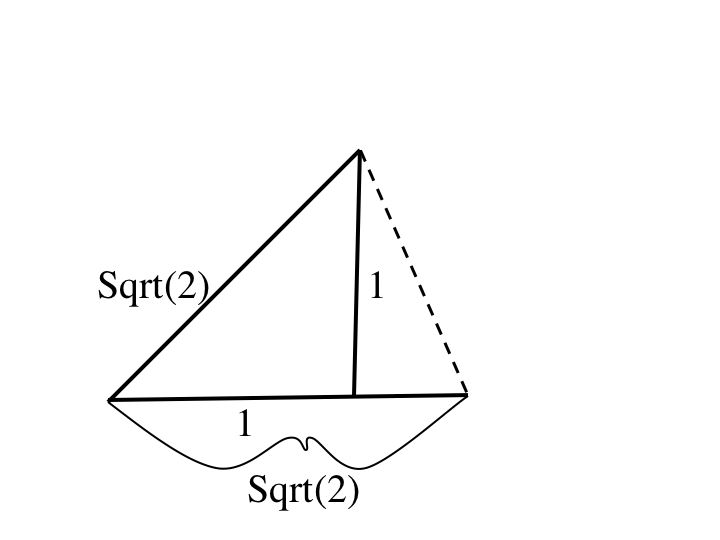
Now copy the length of the hypothenuse and construct a base with length sqrt(2).

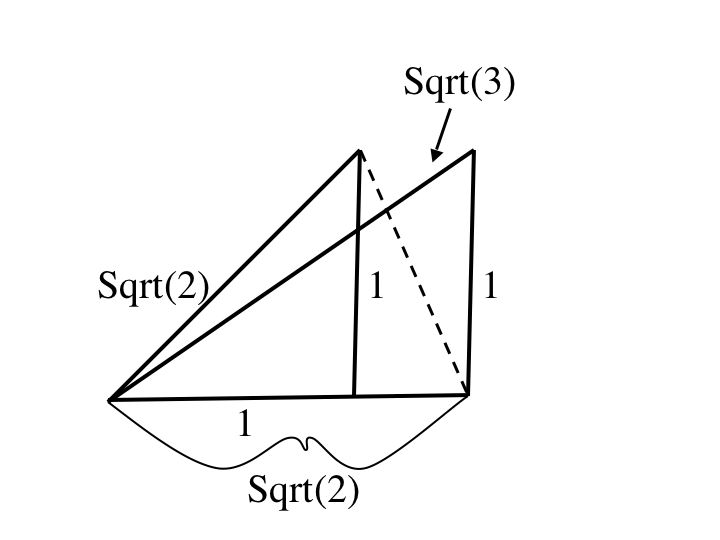
With the length of one leg, sqrt(2), and the length of the other leg, 1, using the pythagorean theorem, (sqrt(2)^2) + (1)^2 = 3, you will find that the hypothenuse has length sqrt(3).

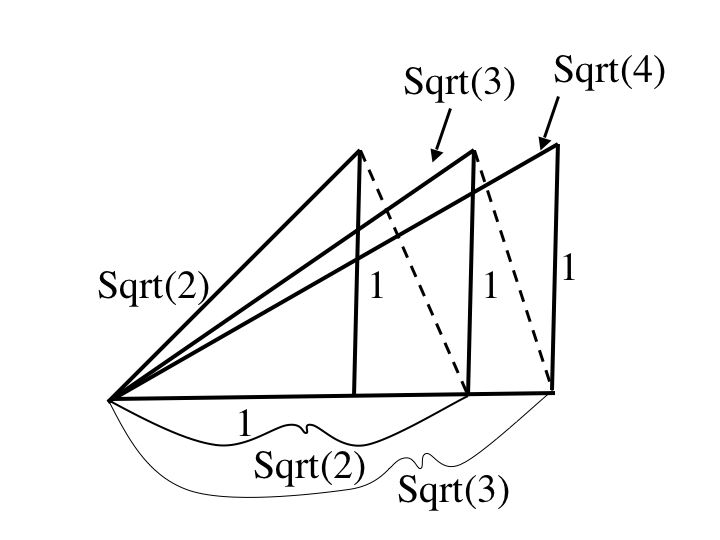
Repeat the above process and you can construct sqrt(4) as well as any square root of a positive integer.

[TOP]

Using the constructible numbers you have found, what Regular Polygons can you construct starting with length 1?

Starting with the length 1:

You can construct a regular triangle.

Start with length 1.

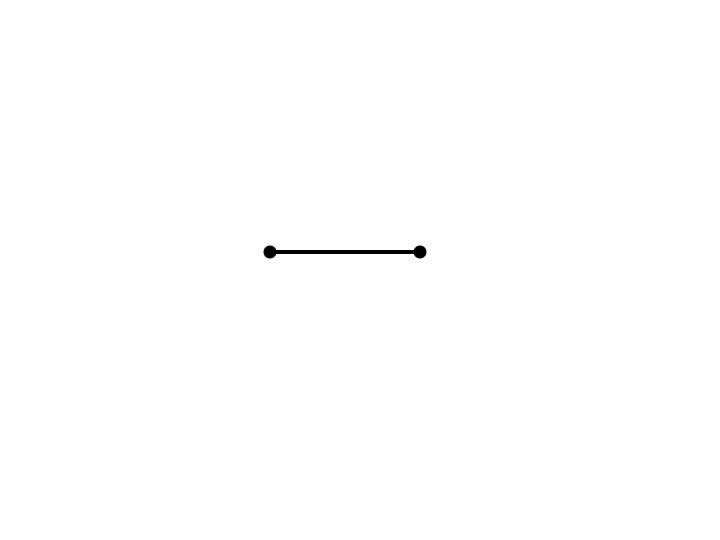
Construct a circle whose center is one of the endpoints of the segment of length 1 and whose radius is length 1.Construct a second circle, whose center is the other endpoint and whose radius is length 1.

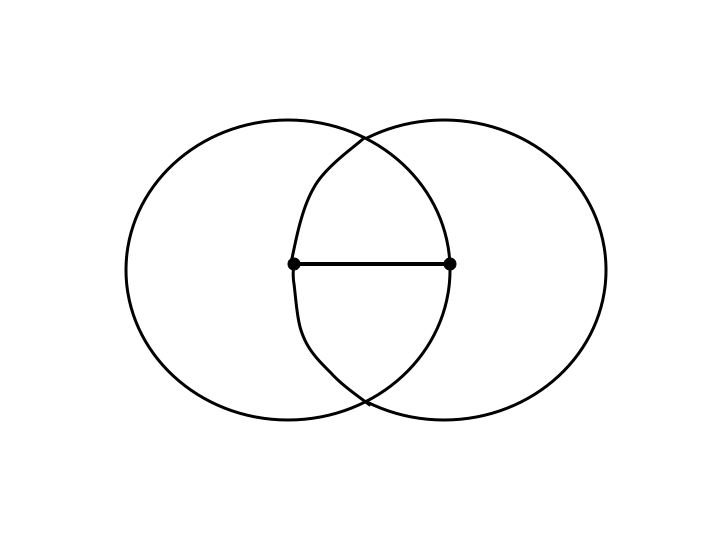
At the point in which these two circles intersect, mark a point.

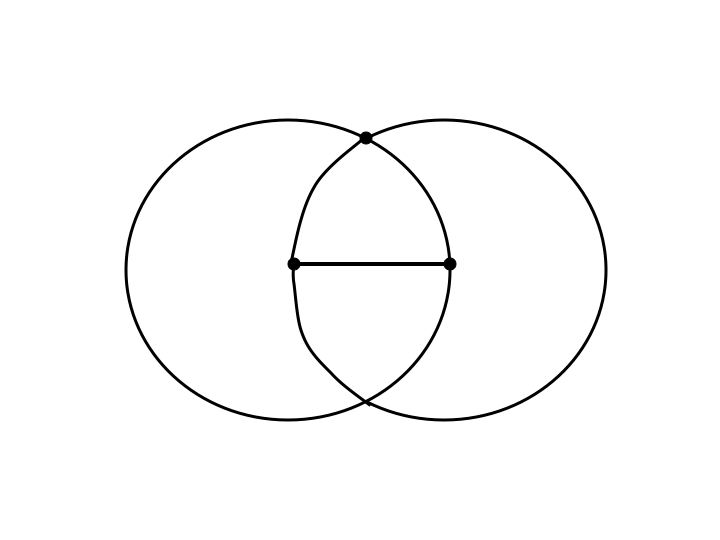
Using your straight-edge connect both endpoints to the mark just made.

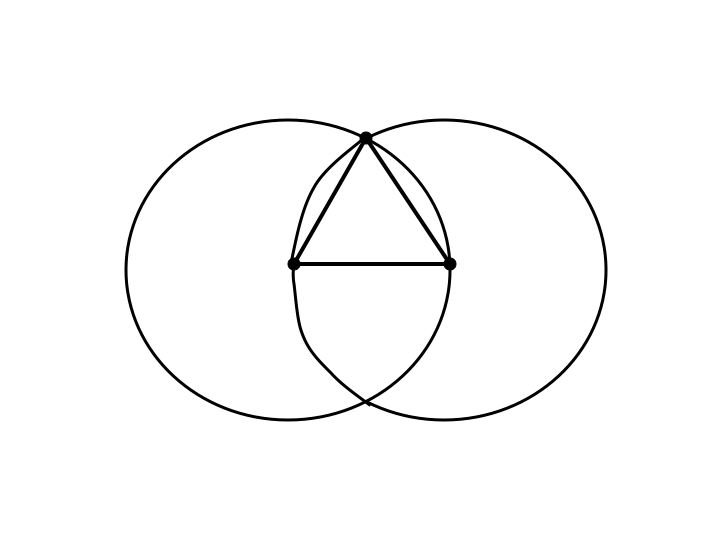
You have just constructed an equilateral triangle.

[TOP]

You can construct a square.

Start with a segment of length 1. Construct the perpendicular bisector of the segment.

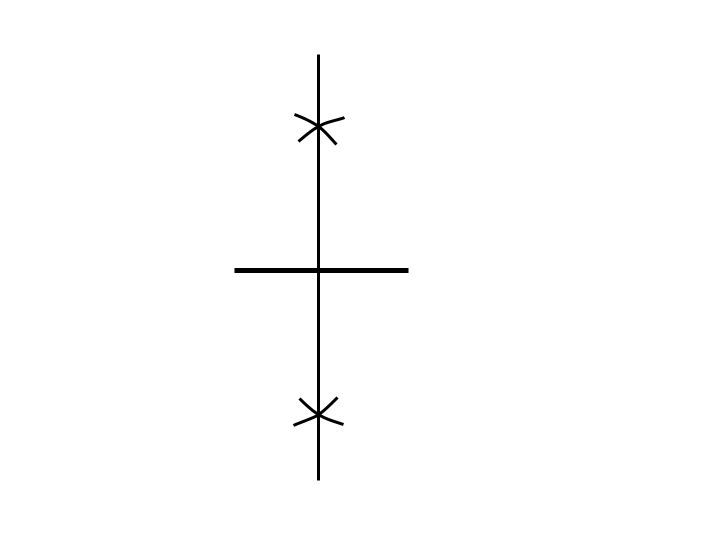
Construct a circle with radius 1/2, using the midpoint of the original segment. Then mark each intersection of the circle and the segments. Using a straight-edge connect each point with the point adjacent to it. You have just constructed a square with sides of length sqrt(1/2).

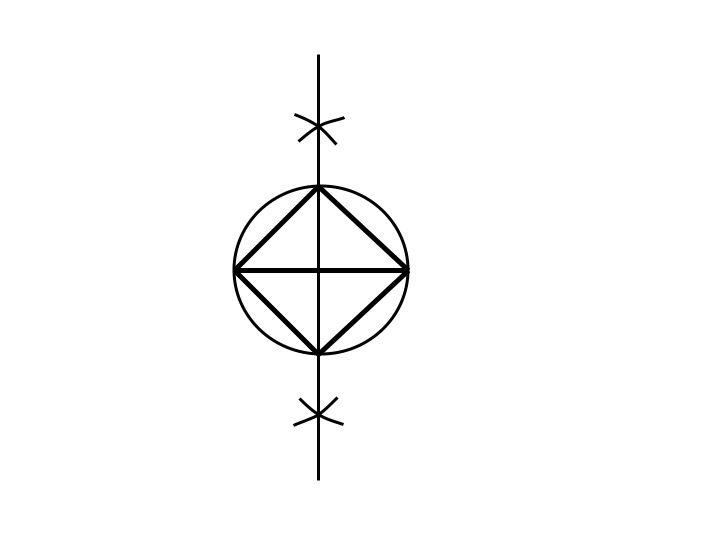
There are many ways to construct a square, this is just one way. Another more complicated version is shown below:

Start with length 1. Construct a perpendicular bisector of the segment.

Mark the midpoint of the original segment. Use the midpoint as the new endpoint and construct a perpendicular bisector of the new segment. Using the midpoint of the original segment as the center construct a circle whose diameter is length 1, the original segment. The radius will be 1/2.

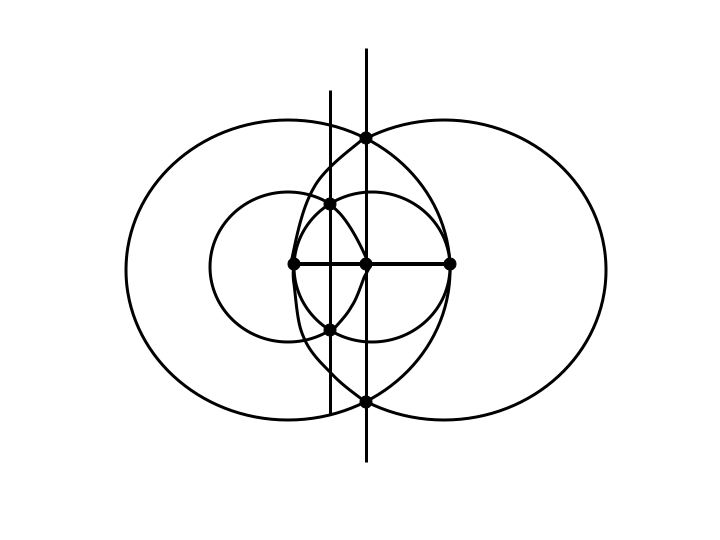
On the perpendicular bisector of the segment, mark where the circle intersects the segment. This too will have length 1/2. Construct a perpendicular bisector of this segment.

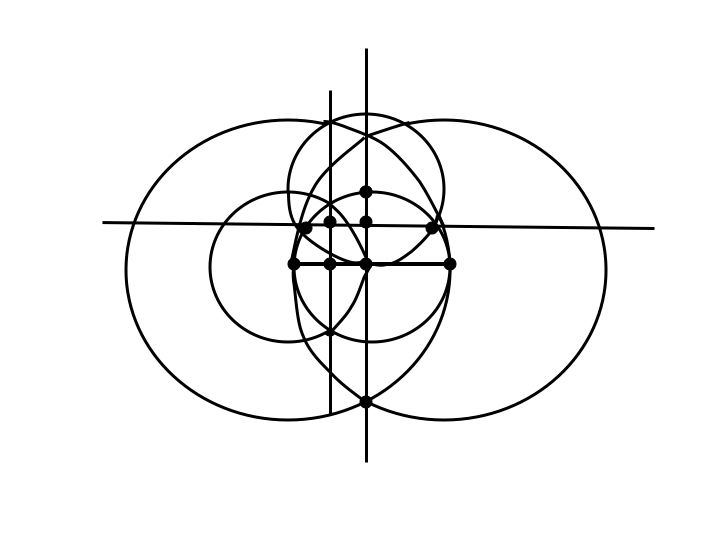
Mark a point at the intersection of the two perpendicular bisectors.

You have created a square whose sides have length 1/4.

There are many ways to construct a square, this is just one way. Another more complicated version is shown below:

[TOP]

Can you construct a pentagon? How?

I will leave this for you to work out on your own.

General Results of Constructing regular (2^n)-gons:

Lets look back at the construction of a square. Why were you able to construct a square, and looking even deeper, why can you construct any regular (2^n)-gon where n is an nonnegative integer?

Using a compass we can construct a circle. A circle can be cut in half by using the straight-edge to construct a segment through the center of the circle. Then take the perpendicular bisector of the segment and we have cut the circumference of the circle into 4 equal lengths. Connect those lengths and you have constructed a square. From the constructible numbers section you know how to bisect an angle. By bisecting the angle you are able to cut the circumference of the circle into 8 equal parts. You can keep doing this and eventually construct any regular (2^n)-gon.

[TOP]