Given a line segment of length 1, what lengths can we construct?

Constructing a Copy of a Segment

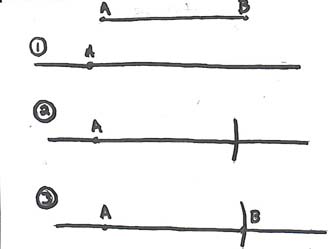
1. Use a straight-edge to draw a line, mark a point on the line and label it A

2. Use your compas to measure the length of the original segment and mark that on the new line

3. Mark and label point B and you have constructed a copy of the original segment

Result: If we start with unit 1, we can continue to copy this line segment to get the set of natural numbers.

[TOP]

Constructing a Copy of an Angle

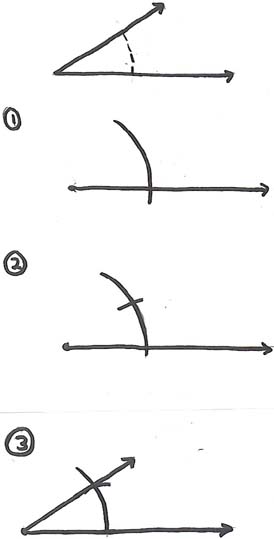
1. Mark a point and construct a ray using a straight-edge and construct an arc using a compass placing the end of the compass on the end of the ray.

2. Using the compass measure the length of the arc on the original angle and mark the length of the arc on the new angle.

3. Using the straight-edge, connect the endpoint of the ray to the point on the arc.

[TOP]

Bisecting a Segment

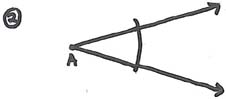
Create two points and label them appropriately.

Connect the points using a straight-edge.

Using a compass, put the end of the compass on a point and create an arc above and below the line. Repeat this process with both points keeping the same compass measurement.

Using a straight-edge draw a line connecting the intersection of both arcs.

The length of the segment AB has now been bisected and the intersection of the two segments are perpendicular to each other.

Result: If we start with the unit 1, we can bisect the segment, thus constructing 1/2. Now we can bisect 1/2 to get 1/4. By continuing this process we can construct the set of numbers {1, 1/2, 1/4, ..., 1/(2^n)}.

[TOP]

Bisecting an Angle

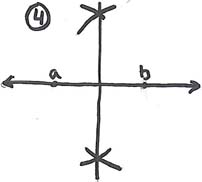
Construct an angle by first creating a point and then using a straight-edge make two rays coming from the point.

Construct an arc intersecting both rays using a compass.

Take both points of intersections of the arc and the rays and construct intersecting arcs.

Using a straight-edge connect the vertex with the intersection of the two arcs.

We have now constructed the bisector of the angle.

[TOP]

Constructing a 45-45-90 Triangle

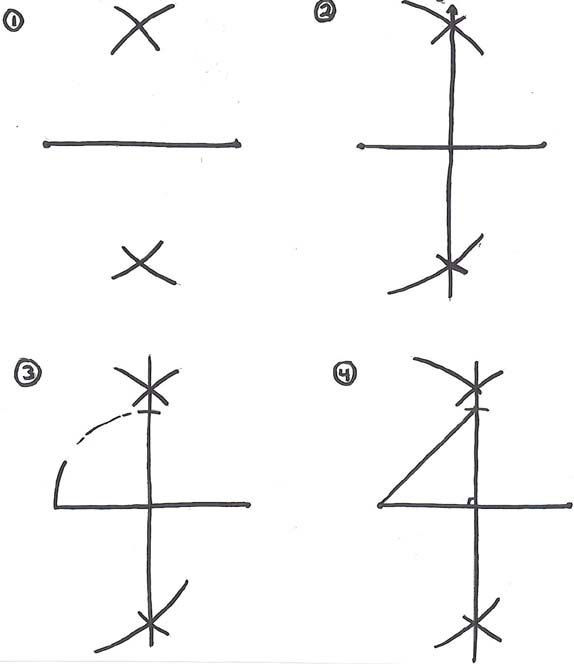
1. Start by constructing a segment.

2. Use the two endpoints of the segment to copnstruct a perpendicular bisector of the segment.

3. Measure the length of the original segment from one endpoint to the intersection of the perpendicular bisector.

4. Mark that length on the perpendicular bisector, using the intersection as one endpoint.

5. Connect the endpoint of the original segment to the mark just made on the perpendicular bisector.