
 |
Tutorial 06 |
Trigonometry |
|
Solving basic trigometric proplems with Excel |
|
 |
back to symbols |
on to graphing |
 |
While Biology laboratories at SMCM don't make extensive use of trigonometry, You will occasionally require its use. It would be a good idea to read at least through the first example and discover the basics of using Excel to evaluate stigmatic functions.
The most important you must know is that in solving trigonometric expressions like sine, cosine and tangent, Excel uses radians, not degrees to perform the calculations! If the angle is in degrees you must first convert it to radians.
There are two easy ways to do this.
You can use the DEGREES(angle) function to convert radians into degrees. For example, DEGREES(PI( ) ) equals 180.
Excel uses several built-in trig functions. Those that you will use most often are displayed in the table below. Note that the arguments for the SIN( ), COS( ) and TAN( ) functions are, by default, radians. Also, the functions ASIN( ), ACOS( ) and ATAN( ) return values in terms of radians. (When working with degrees, you will need to properly use the DEGREES( ) and RADIANS( ) functions to convert to the correct unit.)
| Mathematical Expression |
Excel Expression |
Excel Examples |
| sine: sin(sq) | SIN(number) | SIN(30) equals -0.98803, the sine of 30 radians
SIN(RADIANS(30)) equals 0.5, the sine of 30° |
| cosine: cos(q) | COS(number) | COS(1.5) equals 0.07074, the cosine of 1.5 radians
COS(RADIANS(1.5)) equals 0.99966, the sine of 1.5° |
| tangent: tan(q) | TAN(number) | TAN(2) equals -2.18504, the tangent of 2 radians
TAN(RADIANS(2)) equals 0.03492, the tangent of 2° |
| arcsine: sin-1(x) | ASIN(number) | ASIN(0.5) equals 0.523599 radians
DEGREES(ASIN(0.5)) equals 30°, the arcsine of 0.5 |
| arccos: cos-1(x) | ACOS(number) | ACOS(-0.5) equals 2.09440 radians
DEGREES(ACOS(-0.5)) equals 120°, the arccosine of -0.5 |
| arctangent: tan-1(x) | ATAN(number) | ATAN(1) equals 0.785398 radians
DEGREES(ATAN(1)) equals 45°, the arctangent of 1 |
Below are a few examples of problems involving trigonometry and how we used Excel to help solve them.
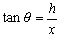
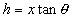 .
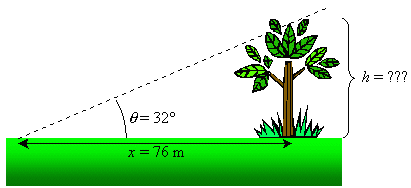
The screen shot below shows how we used Excel to determine that the height
of the tree is 47 m.
.
The screen shot below shows how we used Excel to determine that the height
of the tree is 47 m.
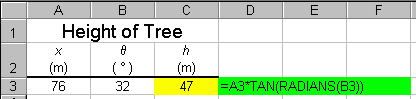
Note the use of the RADIANS( ) function in the above example.
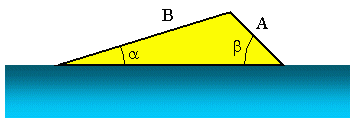 Enough terrestrial biology examples now lets consider an aquatic problem. In
this next example, we wish to know the launch angle, a, of the water ski ramp ( the angle of a coral branch seemed boring) pictured
above. We are given that A = 3.5 m, B = 10.2 m and b = 45.0°. To find a, we can use the Law of Sines which, in this case can be written
Enough terrestrial biology examples now lets consider an aquatic problem. In
this next example, we wish to know the launch angle, a, of the water ski ramp ( the angle of a coral branch seemed boring) pictured
above. We are given that A = 3.5 m, B = 10.2 m and b = 45.0°. To find a, we can use the Law of Sines which, in this case can be written
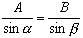
We can rewrite this equation as 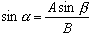 .
Using the arcsine (inverse sine) we can find the angle a using
the equation
.
Using the arcsine (inverse sine) we can find the angle a using
the equation
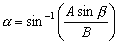
The screen shot below shows how we used Excel to determine that the launch angle of the ramp is 14.04°.

Note the use of the DEGREES( ) and RADIANS( ) function in the above example.
In our final trigonometry example, we will use Excel to examine the trig identity
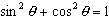 . Even though I cant think of a single
biological reason to do so, this example demonstrates the importance of keeping
units and values in separate cells.
. Even though I cant think of a single
biological reason to do so, this example demonstrates the importance of keeping
units and values in separate cells.
Notice in the screen shot below that this identity holds true when q is given in radians and degrees.

Note: The units for the angle q are placed in different cells than the numbers. If we place the numbers and the units in the same cell, Excel will not be able to decipher the number and therefore we will not be able to reference the cells for use in any equation!
See the complete list of Excel's built-in mathematical
and trigonometric functions and their descriptions.
 |
back to symbols |
on to graphing |
 |
Copyright © 2000, St. Mary's College of Maryland. All Rights Reserved.
Please send comments, problems or request for topics to
Walter I. Hatch
wihatch@smcm.edu
August 11, 2005