The Four-Color Theorem states that any map drawn in the Euclidean plane or on the sphere can be colored with only four colors in such a way that no two adjacent countries are the same color. This result, originally conjectured in 1852, has a colorful and controversial history commensurate with the remarkable difficulty of proving it. On the other hand, it is quite easy to demonstrate that four colors are necessary by drawing a map with four countries, each of which touches all of the others.
On other surfaces, more colors may be required. For instance, on a torus (a doughnut-shaped surface), we have the Seven-Color Theorem, along with many eye-catching ways of proving that seven colors are necessary. Here is a collection of maps on surfaces that are topological tori, each map having seven countries* all of which touch all of the others. Some of them were made and/or designed by me and others are the work of Norton Starr, sarah-marie belcastro, Carolyn Yackel, Moira Chas, Sophie Sommer, Ellie Baker, Skona Brittain, and Faye Goldman.
*except for sarah-marie belcastro’s and one of the bead crochet bracelets, as explained below.
Susan Goldstine, concept by David Lehavi and Tamar Zeigler
 |
 |
 |
 |
This mug, based on a mug designed by David Lehavi and executed by Tamar Ziegler, is the mug I drink tea from at work. (I use my earlier attempts at home.) It dovetails nicely with the old saw about topology being the field of mathematics in which a doughnut is the same as a coffee cup.
The bottom of the mug is white, which allows for a hand-made mug (such as the original I based this on) to be fired with an unglazed surface touching the kiln. All the other colors touch white around the base of the mug. The interior of the mug is blue, and the colors other than white all touch blue around the top of the mug. Red, orange, and yellow wrap around the handle, and green, blue, and purple wrap around the body. To verify that all pairs of colors touch, it only remains to check that green and purple both touch red, orange, and yellow, and this can be observed in the photographs above.
Because I haven’t worked with clay since high-school art classes, I made this mug at a paint-your-own-pottery studio. In order to produce sharp boundaries, I surrounded each color region with masking tape and cut the shape out with a craft knife before applying the glaze. I have since discovered that it is much easier to paint the regions carefully by hand, applying the glazes in order from lightest to darkest.
Susan Goldstine
 |
 |
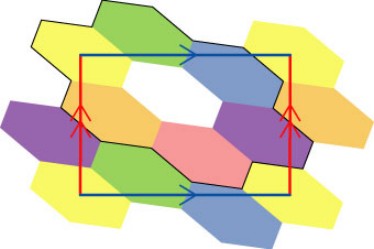
In topology, a standard method of conceptually constructing a torus is to take a rectangle and glue together the pairs of opposite edges. Usually, one imagines stretching the rectangle before gluing to make a traditional rounded doughnut shape, but in this model, an actual rectangle of fabric is sewn together to make this nearly flat torus. The rectangle is made up of seven congruent hexagons, each of which borders all of the others.
It is not easy to see all at once how all of the colors in this torus fit together, but the model can be flattened out around each of the seven hexagons separately. In the photo array below, each hexagon in turn is shown surrounded by the other six.

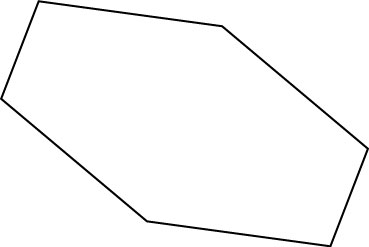
To make your own version of this model, print out the hexagon below, enlarge it to whatever size you desire, and cut seven of these hexagons out of fleece or some other fabric that will not unravel when you cut it. Stitch the hexagons together as shown in the colored diagram.
 |
 |
The hexagon has three different angles, even though two of them are very close to each other. Be careful not to flip a hexagon and swap these two angles.
 |
 |
The first time I tried to make this model, I inadvertently introduced a full twist in the rectangle before stitching it shut. While the twisted model, pictured above, is not as well-behaved as the flat model, I kind of like the sense of roundedness and fullness the twist gives the torus.
Susan Goldstine, from the pattern by David King
 |
 |
 |
 |
Amazingly, there is a polyhedron, called the Szilassi polyhedron, that has seven hexagonal faces, each of which touches each of the others. The polyhedron, which Szilassi discovered in the 1970s, is a topological torus that is incredibly hard to photograph clearly but really fun to make.
I constructed this Szilassi polyhedron out of poster paper and tape using the pattern from David King’s Hall of Hexagons.
Norton Starr
 |
 |
Above are photographs of the two sides of Norton Starr’s painted hydrostone torus depicting the Ungar-Leech map. One of the nice features of this map is that you can see all seven colors touching each other in a single view, the left-hand view above. This model is featured on the cover of David Gay’s book Explorations in Topology: Map Coloring, Surfaces and Knots.
sarah-marie belcastro and Carolyn Yackel
As part of their incredible work in mathematical fiber arts, sarah-marie belcastro and Carolyn Yackel created the two tori below. The upper torus was knit by belcastro, and the lower torus was crocheted by Yackel. In order to adapt the seven-color torus to yarn-based media, they had to develop their own seven-color configuration.

In fact, these torus maps are duals of each other. While Yackel’s torus is a map with seven countries each of which shares a border with all the others, belcastro’s is a graph with seven vertices (only three of which are visible in the image above) each of which is connected by an edge to all of the others. In more mathematical terms, the upper torus represents an embedding of the complete graph on seven vertices (K7) on the torus. There is a one-to-one correspondence between belcastro’s vertices and Yackel’s countries, and a matching correspondence between belcastro’s edges and Yackel’s borders between countries.
Yackel and belcastro have also designed a pattern for an eight-colored surface of uniform curvature that is a topological two-holed torus.
Moira Chas
 |
 |
Moira Chas has crocheted a prodigious collection of seven-color tori as well as maximal colorings of various multi-hole tori. Here is a small sample of her work; you can see much more at her Map Coloring with Crochet page and her feature column for the American Mathematical Society.
Sophie Sommer
In a similarly crafty vein, Sophie Sommer developed her own pattern for a seven-colored beaded crochet bracelet, a feat made all the more impressive by the fact that she invented the pattern during her senior year of high school. One of Sommer’s bracelets is pictured below.

Sommer has graciously shared her pattern for this bracelet.
Sophie Sommer, Ellie Baker, and Susan Goldstine
Sophie Sommer, Ellie Baker and I developed some refinements and expansions of Sommer’s first seven-color torus bracelet, displayed in our joint artwork Seven-Color Torus Series in Bead-Crochet, which was part of the Joint Mathematics Meetings Exhibition of Mathematical Art in 2010. Like sarah-marie belcastro’s knitted torus above, the bracelet in the bottom right depicts an embedded complete graph on seven vertices.

The patterns for three of these bracelets (including Sommer’s original pattern linked above) appear in the book Crafting Conundrums: Puzzles and Patterns for the Bead Crochet Artist, by Baker and me.
Skona Brittain
 |
 |
Continuing the fashion theme, Skona Brittain designed and made this seven-color-map belt. She deliberately arranged the countries so that the colors she most likes to wear appear on the outside of the belt.
Ellie Baker
This is an infinity scarf that Ellie Baker made with fabric of her own design printed by Spoonflower. The scarf is a rectangle of fabric with opposite edges sewn together, giving an essentially "flat" torus with a rendition of the Ungar-Leech map.

Here is the pattern for the fabric rectangle before sewing.

Faye Goldman

Above is Seven Sided Seven Color Torus, an origami artwork by Faye E. Goldman from the 2015 Joint Mathematics Meetings Art Exhibition. Goldman used over 3200 strips of ribbon, folded with the Snapology technique developed by Heinz Strobl.