
| Rhombic Dodecahedron dual to cuboctahedron  | Rhombic Triacontahedron dual to icosidodecahedron  | |
| Cube (Rhombic Hexahedron) dual to tetratetrahedron  |
If you are not familiar with duals of solids, read this first.
There are one-to-one correspondences between the faces of a polyhedron and the vertices of its dual, between the edges of a polyhedron and the edges of its dual, and between the vertices of a polyhedron and the faces of its dual. In constructing the duals to semi-regular solids that are not regular, we may encounter a geometric difficulty not present in the regular case. Sometimes the centers of the faces with a common vertex in the semi-regular solid do not lie in a single plane, even though these are supposed to be the vertices of a single face of the dual. In the cases of the "tetratetrahedron" (which is regular) and of the cuboctahedron (which is not), this problem does not arise. However, in the case of the icosidodecahedron, it does. We may construct the icosidodecahedron dual by moving the dual vertices inside the triangular faces towards the center of the icosidodecahedron, thereby flattening the dual's faces into planar rhombi. The result is the rhombic triacontahedron, also known as Kepler's solid.

| Rhombic Dodecahedron dual to cuboctahedron  | Rhombic Triacontahedron dual to icosidodecahedron  | |
| Cube (Rhombic Hexahedron) dual to tetratetrahedron  |
Another way to construct the rhombic triacontahedron is to erect a pentagonal pyramid on each face of a dodecahedron in such a way that the triangles on either side of each edge of the dodecahedron align to form a rhombus. Conversely, if you use blue Zometool edges to connect the vertices of the triacontahedron that have three adjacent edges, you get a dodecahedron. It should not come as a surprise that you can similarly erect triangular pyramids on the faces of an icosahedron, and that if you use (longer) blue Zometool edges to connect the vertices of the triacontahedron that have five adjacent edges, you get an icosahedron. A similar scheme connects the rhombic dodecahedron to the cube and to the octahedron. Moreover, a cube (whose faces are right-angled rhombi, otherwise known as squares) may be obtained by attaching a right-angled pyramid to each face of a tetrahedron, and there are two tetrahedra that may be obtained by connecting vertices of the cube. This final fact is thoroughly discussed elsewhere in these pages. With additional blue and green Zometool edges, each of these constructions can be modeled.

|

|
The rhombic triacontahedron and the rhombic dodecahedron are not themselves Archimedean solids even though their duals are. However, they do each have the property that there is a symmetry taking any face to any other face, which is the dual property to that of an Archimedean solid. One consequence of this fact is that if you connect the centers of the faces of the rhombic triacontahedron, you do get an icosidodecahedron, even though the reverse is not quite true.
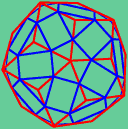
Another way to construct the icosidodecahedron is to connect the midpoints of the edges of an icosahedron or of a dodecahedron. If instead you connect the midpoints of the edges of the rhombic triacontahedron, you obtain the solid diagrammed in blue above, which is essentially a rhombicosidodecahedron, but with each square replaced by a golden rectangle. Zometool aficionados may recognize this polyhedron as the shape of a Zometool vertex (pictured below). One of the cool features of the Zometool system is that you can actually make a larger model of the vertex polyhedron out of blue edges.