What the Origami Means
- The faces of a polyhedron are its flat sides, each of which is a polygon.
- The edges of a polyhedron are the edges of its polygonal faces.
- The vertices (singular: vertex) of a polyhedron are its corners.
Platonic and Archimedean Solids
- All of its faces are identical regular polygons. (A polygon is regular if all its sides are equal and all its angles are equal.)
- The number of faces around each vertex is the same.
There are only five regular solids, all of which are pictured
below.
The Greek names of the solids refer to the number
of faces they have: "tetra-" means four, "octa-" means eight,
"dodeca-" means twelve, and "icosa-" means twenty.
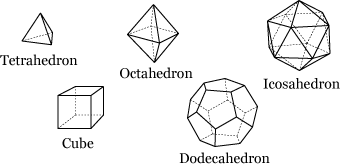
A semi-regular or Archimedean solid is characterized by the following properties:
- All of its faces are regular polygons, although they are not necessarily all identical.
- The configuration of polygons around each vertex is the same.
Clearly, each of the regular solids is also semi-regular, but there are many additional solids that meet these looser conditions. Most of them are closely related to the regular solids and can be constructed by cutting, combining, or distorting their Platonic relatives. Many of these hybrid solids are modeled in this display.
Polyhedra Represented by the Hanging Models


Remark: The
photograph above was taken eight years
after the display was installed. The rhombicosadodecahedron
model, whose unsupported pentagons make it the least stable of the
hanging models, has sagged considerably over the years.
The truncated polyhedra are formed by slicing the corners off of
the tetrahedron, the octahedron, and the icosahedron. In each
case, the triangular faces of the original solid become hexagons.
Notice that the truncated icosahedron is the pattern of stitches
on a soccerball.
To form a rhombicuboctahedron, imagine taking a cube and pulling its six square faces away from each other as though the edges of the cube were made of elastic. Each edge of the cube turns into another square, and each vertex turns into a triangle, and the resulting solid is the rhombicuboctahedron. The same solid results if the faces of an octahedron are pulled apart; to understand why, see the description of dual polyhedra below. A similar relationship connects the rhombicosidodecahedron to a dodecahedron or an icosahedron. Pulling apart the triangular faces of a tetrahedron yields the cuboctahedron, further described below.
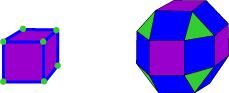
I have devised a Zometool model of the rhombicosidodecahedron which illustrates its relationship to the icosahedron and the dodecahedron.
Now, once again imagine pulling apart the faces of a cube, and imagine that the original square faces of the cube and the triangles that were once the vertices of the cube are rigid like pieces of metal and are joined at the corners. If the rigid squares are simultaneously twisted in just the right way, the former edges of the cube will collapse from squares into pairs of equilateral triangles, and the new solid will be a snub cube. The other snub solids arise in a similar fashion.

Here is another set of snub solid models which is colored differently than but otherwise identical to the one in the Amherst display.

Dual Polyhedra

Remark: Since I am not expert in devising original origami forms, I generally assemble origami modules invented by other people into mathematical models that interest me. There are only two bits of paper folding in this display for which I can even remotely take credit, and both are pictured above. First, I made the straightforward discovery that Tomoko Fuse's Plain Open Frame Unit (the most prevalent module in the display) can be assembled with some of its creases reversed to form support struts for pentagonal faces (notice the yellow struts in the largest model above). This method remains the best technique I know for modeling solids that contain pentagonal and triangular faces. Second, for the intersecting dual pair models in the back row, I had to develop the yellow dodecahedron-corner inserts to complete the set, which otherwise consists of units from Tomoko Fuse's arsenal. The inserts use a trigonometric approximation which I later discovered to be related to the approximation used in the dodecahedron units shown below.
The centers of the faces of any regular polyhedron form the vertices of another regular polyhedron. For example, if we take the centers of the faces of a cube and connect them with edges and faces, we obtain an octahedron. For this reason, the octahedron is called the dual of the cube.
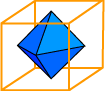
In fact, the reverse is also true; if we take the centers of the faces of an octahedron and connect them with edges and faces, we get a cube.
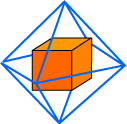
In the same fashion, the icosahedron and dodecahedron are duals, and the tetrahedron is its own dual.
Returning to the octahedron inscribed in the cube, we can imagine
gradually enlarging the octahedron until its edges just touch the
edges of the cube. (Of course, the same can be done with the cube
inside the octahedron.) The resulting figure, pictured below, is
one of the three intersecting-dual-pair models above.
[Back row, left to right:
Icosahedron/Dodecahedron, Octahedron/Cube, Tetrahedron/Tetrahedron]
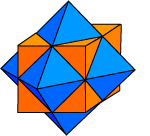
By taking the dual-pair solids and chopping
off
all of the pyramidal
protrusions, we obtain the icosidodecahedron, the cuboctahedron,
and the octahedron, semi-regular solids which contain all of the
faces of two dual Platonic solids. Alternately, each figure can be
obtained in two ways (one, in the octahedron's case) by truncating
a single regular solid. The cuboctahedron can be formed either by
slicing the corners off of a cube to create the eight triangles of
an octahedron or by slicing the corners off of an octahedron to
create the six squares of a cube.
[Front row, left to right:
Icosidodecahedron, Cuboctahedron, "Tetratetrahedron" (Octahedron)]

The icosidodecahedron, the cuboctahedron, and the "tetratetrahedron" have duals of their own. The geometry of the Zometool construction system makes it straightforward to construct models of these Archimedean duals.
The edges of an icosidodecahedron form six regular decagons, each of which bisects the icosidodecahedron. This is one reason that collapsible Hoberman Spheres can easily be constructed as icosidodecahedral linkages. Similarly, the edges of a cuboctahedron form four regular hexagons, and the edges of an octahedron form three squares.
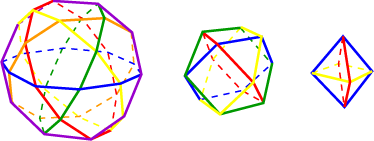
Symmetries of Polyhedra
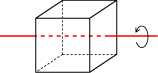
A symmetry of a polyhedron is a way of moving the polyhedron so that it occupies the same physical space as before it was moved. As an example, consider the symmetries of the cube. A cube can be rotated 90°, 180°, or 270° around an axis passing through the centers of two opposite faces of the cube,
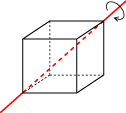
or it can be rotated 120° or 240° around an axis passing through two opposite vertices of the cube,
or it can be rotated 180° around an axis passing through the midpoints of two opposite edges of the cube.
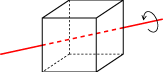
In fact, these comprise all of the symmetries of the cube except for the mundane but mathematically important move of leaving the cube where it is.
The symmetries of a polyhedron reflect its structure and regularity. A polyhedron is regular if there is a symmetry taking any face to any other face and a symmetry taking any vertex to any other vertex, and a polyhedron with regular faces is semi-regular if there is a symmetry taking any vertex to any other vertex.
Other types of geometric figures also have symmetries. To play around with symmetries in the plane, check out the University of Minnesota Geometry Center program Kali, which lets you make patterns that correspond to each of the 17 wallpaper groups.
Permutation Groups
A permutation is a way of rearranging a finite set of objects. For instance, we can define a permutation σ of four objects by
 BCAD,
BCAD, meaning that σ puts the first letter into the third position, puts the second letter into the first position, puts the third letter into the second position, and leaves the fourth letter fixed.
If we have two permutations of the same number of objects, we can combine them to form a third permutation. Taking the permutation
 BADC,
BADC, which swaps the first and second letters and swaps the third and fourth letters, and the permutation σ above, we can create a new permutation, which we will denote σ * σ, by performing σ and then τ. That is,
 BCAD
BCAD  CBDA.
CBDA. The permutations of a fixed number of objects together with the operation * have the mathematical structure of a group. Below are enumerated the properties that make the permutations into a group; offered for comparison are the corresponding properties of the more familiar group of real numbers with the operation +.
| Associativity | |
|---|---|
| (α * β) * γ = α * (β * γ) | (a + b) + c = a + (b + c) |
| Identity | |
| The identity is the permutation ε
which moves nothing: ε * α = α * ε = α |
The identity is 0: a + 0 = 0 + a = a |
| Inverses | |
| Every permutation α has an
inverse
permutation β, obtained by reversing all of the moves of α, such that α * β = β * α = ε (For example, the inverse of τ
above
is τ, |
Every number a has an additive inverse -a, such that a + (-a) = (-a) + a = 0 |
A major difference between a group of permutations and the additive group of numbers is that while the latter is commutative, i.e., a + b = b + a, the former is usually not:
 BADC
BADC  ADBC,
ADBC, which is not the same as σ * τ.
The group of all permutations of a set of n objects is called the symmetric (permutation) group on n letters, denoted Sn. There is a smaller group contained in Sn called the alternating (permutation) group on n letters, denoted An, which consists of only the even permutations.
A permutation is called even if it can be acheived by swapping pairs of objects an even number of times. For instance,
 CAB
CAB is even because it is obtained by swapping the first and second letters and then the first and third letters, while
 BAC
BAC is not even. It turns out that exactly half of the permutations in any given Sn are even.
Permutations and Symmetries
The models above are colored to show an equivalence between the symmetry groups of the regular polyhedra and certain permutation groups. In each case, the symmetries of the polyhedron correspond to either all permutations of the colors or the even permutations of the colors, as follows.
| Polyhedron | Symmetry Group |
|---|---|
| Tetrahedron | A4 |
| Cube | S4 |
| Octahedron | |
| Dodecahedron | A5 |
| Icosahedron |
Remark: Opposite corners of the cube below (and opposite faces of the octahedron below) have the same color.

Consider as an example the model cube, in which the white portions should not be counted as a color for these purposes. The permutation
 GRBY
GRBY corresponds to a rotation by 90° around an axis passing through the centers of the front and back faces, the permutation
 RYGB
RYGB corresponds to a rotation around an axis passing through the red vertices, and the permutation
 GBYR
GBYR corresponds to a rotation around an axis passing through the two red-green edges. That the symmetry group of the cube is S4 means that any permutation of the colors can be achieved by some symmetry of the cube and vice versa.
Remark: The twisted dodecahedron model in the photo above, made with Thomas Hull's PHiZZ Unit, has been replaced by the more accurate dodecahedron model pictured below, made with an ancestor of the PHiZZ Unit that was developed by Robert Neale. The folding pattern is similar to that of the PHiZZ Unit and experienced folders should have little trouble reproducing it.

Symmetries and Embeddings
We can use a similar construction to relate the symmetry groups of the tetrahedron and of the cube. As shown below, it is possible to inscribe a tetrahedron in a cube in such a way that the vertices of the tetrahedron are four of the eight vertices of the cube.
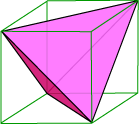
The other four vertices of the cube form the vertices of another tetrahedron; this can be seen by looking at the model of two intersecting tetrahedra among the dual polyhedra models above, in which the edges of the two tetrahedra are the diagonals of the square faces of the circumscribed cube. It is clear that every symmetry of the cube will either cause both tetrahedra to occupy the same space as before or exchange the positions of the two tetrahedra. What is not as clear but equally true is that it is precisely the symmetries of the cube leaving the two tetrahedra unswapped (namely the identity, rotations through pairs of opposite vertices, and rotations by 180° through centers of opposite faces) that correspond to the even permutations in S4. In other words, the symmetries of each tetrahedron sitting in the cube correspond to the permutation group A4 contained in S4.


The model above, made after the Amherst installation, further illustrates the relationships between the cube, the octahedron, and the tetrahedron. It consists of four copies of a simple origami octahedron (if you know any origami, try your hand at making such an octahedron by fitting together six waterbomb bases), connected with a simple linkage. The resulting figure fits naturally inside a tetrahedron: in fact, its convex hull (think of this as the shape you would get if you wrapped the model in plastic wrap) is a truncated tetrahedron. The origami form can be viewed as six intersecting rectangles, each of which is a doubled square. Although it is difficult to see in these photographs, the solid bounded by these six rectangles is a cube. One vertex of the cube is resting on the ground and the opposite vertex is in the center of the top triangle in the left picture. Four of the eight vertices of this central cube are the centers of the four octahedra and form the vertices of a tetrahedron parallel to the tetrahedron circumscribing the model.
Three-dimensional space can be tiled by octahedra and tetrahedra with a fixed edge length; in the tiling, each triangular face has an octahedron on one side and a tetrahedron on the other. The model above this text represents a tetrahedron surrounded by four octahedra within this tiling. Adding ten more tetrahedra yields the larger tetrahedron described above. In a similar vein, the intersecting dual tetrahedra model can also be viewed as an octahedron surrounded by eight tetrahedra and may be interspersed with octahedra to fill space.
Another way to see that the symmetry group of the
dodecahedron
is A5 is to observe that the twenty vertices of the
dodecahedron
are the vertices of five intersecting tetrahedra, and that the
symmetries of the dodecahedron correspond to the even permutations
of these tetrahedra. For pictures of the five tetrahedra and
instructions on how to make an origami model of them, go to Thomas Hull's
Instructions on his Origami Mathematics Page.
If you have any experience with modular origami, you must
make Hull's model; the diagrams on Hull's page don't
do justice to how stunning the model looks when
rendered in bright, contrasting colors (though these
photos come close).
As a corollary to the embedding of a tetrahedron in a cube, it is also possible to find five cubes in a dodecahedron that are permuted by the symmetries of the dodecahedron. The edges of these cubes are the sixty diagonals of the pentagonal faces of the dodecahedron. Below are pictures of the model in the lower right corner of the Amherst origami display, which shows the cubes through a combination of paper and thread. My thanks go to Irene Starr for these photographs.
 |
 |
Furthermore, it is possible to inscribe an octahedron in a tetrahedron (in fact, if you stellate an octahedron, you get the intersecting tetrahedra modeled above) and to inscribe an icosahedron in an octahedron. If you combine all of these constructions, you get a nifty nesting of all five regular solids. Here are two non-origami models of this arrangement.
 |
 |
Drinking Straws |
Zometool |
Zometool now has a package called Kepler's Obsession, which contains all the parts you need to make the model above but with different colors for each regular solid. If you are a Zometool enthusiast, you may want to make this investment; even if you do not mind the poor coloring of the model above, you need some of the rarer lengths of green edges to complete it.
