Definition

Constructible Numbers

The real number a is said to be a constructible number if |a|, the absolute value of a, can be constructed using a compass and a straight-edge, letting 1 be the unit length.

Properties

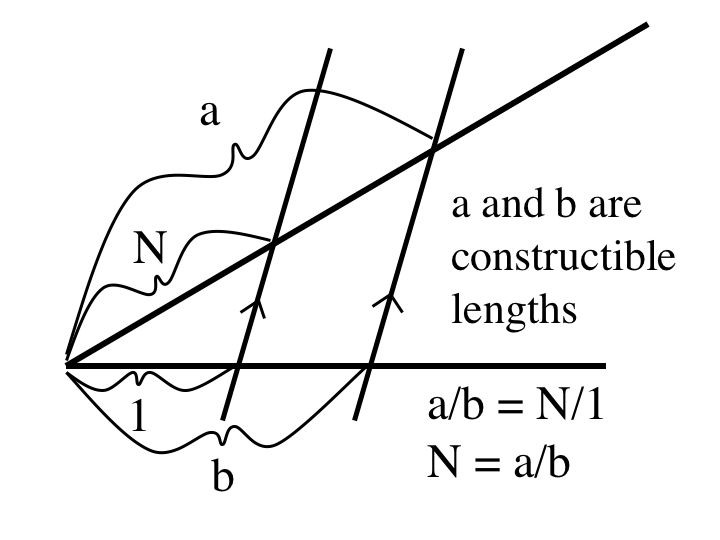
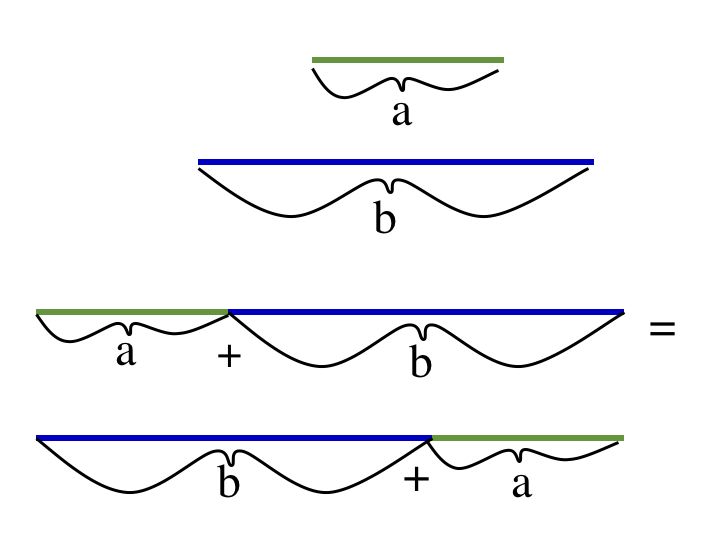
Let a and b be constructible:

a + b is constructible

ab is constructible

a/b is constructible

The square root of 2 is constructible since 1 is constructible.

Show that if a is constructible, sqrt(a) is constructible.

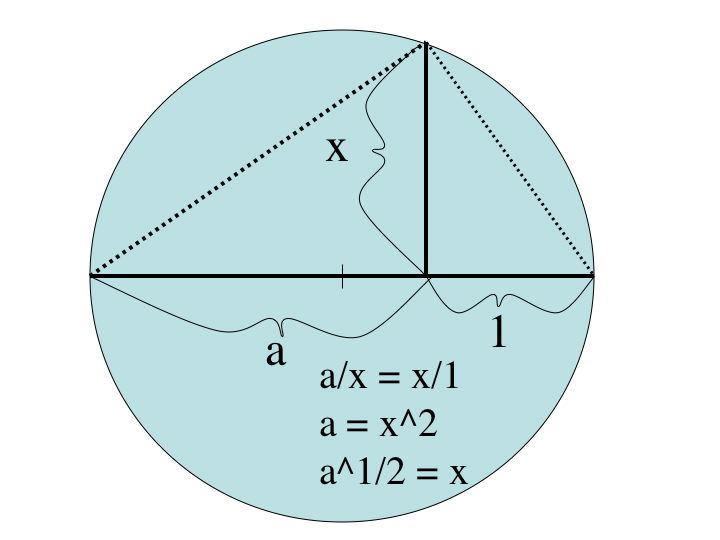
Using a compass and a straight edge, a circle and its diameter can be constructed. From that we can construct x. Similar triangles allow a/x = x/1. So x = a^1/2 and a^1/2 can be constructed.

[TOP]

The constructible numbers form a subfield of the real numbers

Proof

Given a unit 1, we know that we can construct a+b and ab, so we know that the constructible numbers are closed. With some added work we can also gain associativity and the distributive laws. 0 is contained in the set of constructible numbers so their is an identity. We can construct a-b so we can construct an additive inverse. We can also show commutativity within our set under both addition and multiplication.

The last thing we need to show is that the set is a division ring. Since we can construct a/b for all b 0, we are able to construct the inverse of any rational number b/a, a 0. 0 acts as its own inverse.

So the constructible numbers forms a subfield of real numbers.