Symmetric Groups

[Triangle] [Square] [Tetrahedron] [Cube]

A(S) is the set of 1-1 mappings of S onto itself. If S is a finite set with say n elements then A(S) is called a symmetric group of order n denoted S_n.

The elements of S_n are called permutations of S.

Elements in the Symmetry Group of an Equilateral Triangle

Let's first look at the types of transformations we can perform on an equilateral triangle:

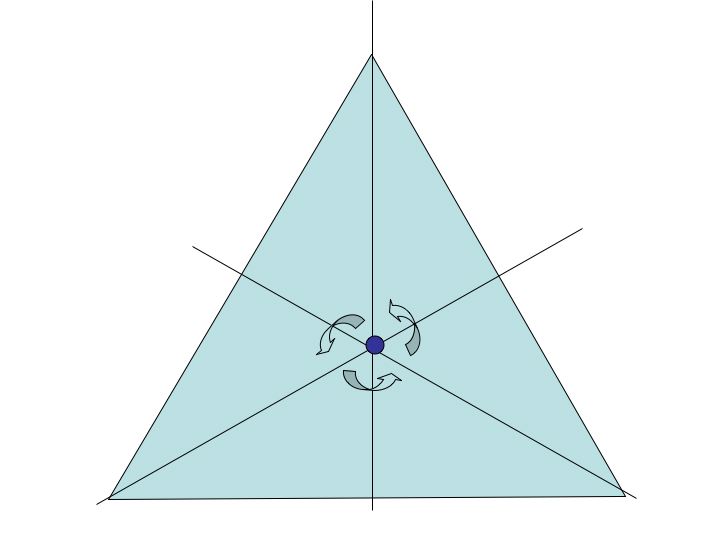
Rotations: If we rotate the triangle counterclockwise 120 degrees around the center. We rotate the triangle once by 120 degrees, we do not get back to the original triangle. We rotate the triangle another 120 degrees, we still don't get back to the original. We rotate it 120 degrees for a third time and we do get back to the original. From this we get r_1 (rotating the preimage 120 degrees around the center), r_2 (rotating the preimage 240 degrees around the center) and the identity.

Reflections: If we construct a line that intersects an edge with the midpoint of the opposite side, we will be able to reflect over that line. Since there are three edges we can create create a perpendicular bisector of the sides intersecting each edge, thus giving us 3 lines of reflection which we will label as |, \, and /.

Translations: Translating the triangle will get us not provide us with any symmetries of an equilateral triangle.

So there are six elements in the symmetry group of an equilateral triangle.

How do I know that these 6 elements form a group?

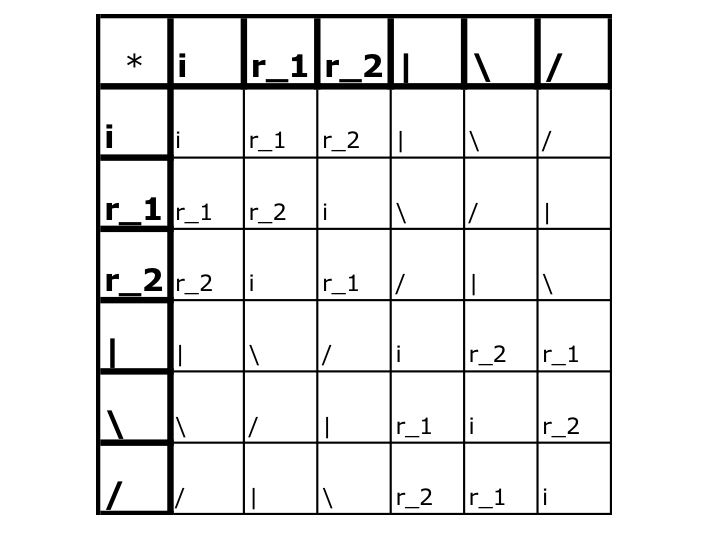
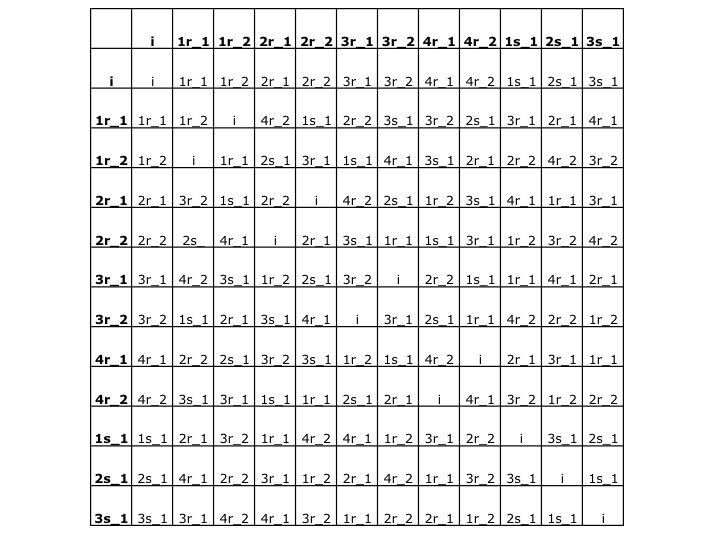
Let's look at the chart. How do we read the chart? Let's try an example. r_1*|.

Start on the left column. Scroll down until we find r_1. Now place mark it for a moment. Look at the top row. Scroll over until we find |. Now find where the row starting with r_1 and column starting with |. Follow these over and down until we reach the same box. What do we reach? \. So r_1*| = \. Let's check to see if we are correct. First rotate the triangle counterclockwise 120 degrees. Now on this new image, reflect over the vertical line intersecting the top corner and the midpoint of the opposite edge. What have we demonstrated? The result is the same as if we had just applied \. So we have demonstrated that if we take the composition of two elements we will get a third element, which is the same as if we applied the rotation or reflection associated with the third element.

Is there closure?

Choose a,b in set of symmetries of a traingle. Is a*b still in the set? If you look at the cahrt, the answer is yes. No mater which two elements we choose we always get something still in the set.

Associativity?

Using the chart, a lot of paper and a pencil we can find that the associativity property holds. Take for instance (r_2*r_1)*| = i*| = | = r_2(\) = r_2*(r_1*|). Labeling each corner of the triangle will help you identify associativity. Choose two elements. Combine two elements to get the third. Now look at the second to elements, combine those first, and then combine the first element with the elemet you created from combining the second and third. If we have labeled the trianlge we will see that we have come up with the same element. Since this is a finite set, we can show this set holds associuativity just by doing all the possible combinations.

Identity?

By looking at the first row or first column of the chart we can see that i is the identity.

Inverse?

Yes. r_1 and r_2 are inverses of each other and |,\, &/ are there own inverses.

So the set of symmetries of an equilateral triangle do form a group which we call the symmetry group of an equilateral triangle.

Subgroup

S = {r_1, r_2, i}

Closure:

r_1*r_2 = i

r_2*r_1 = i

r_1*r_1 = r_2

r_2*r_2 = r_1

Associativity:

These properties hold from the group so we do not need to check for associativity.

Identity:

The idenity element from the group is in the subgroup and this property holds from the group so we do not need to check to see if the identity holds.

Inverse:

r_1*r_2 = r_2*r_1 = i

Other Subgroups

G = {|, i}:

|*| = i, |*i = i*| = |

H = {\, i}

\*\ = i, \*i = i*\ = \

I = {/, i}

/*/ = i, /*i = i*/ = /

[TOP]

Elements in the Symmetry Group of a Square

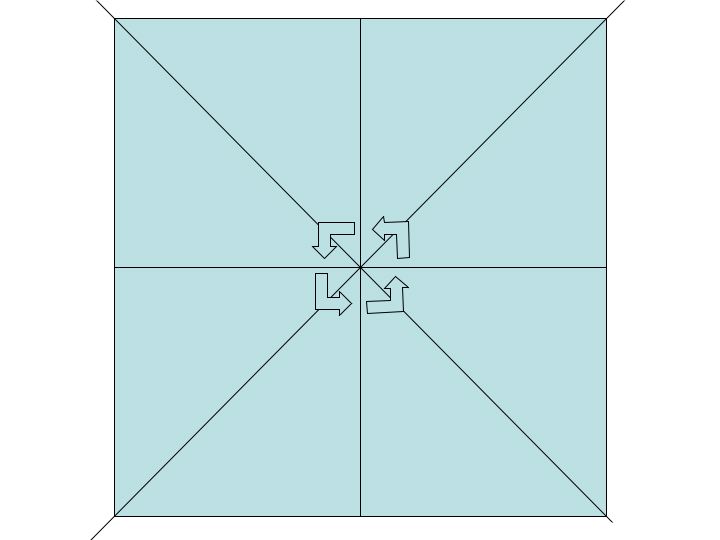
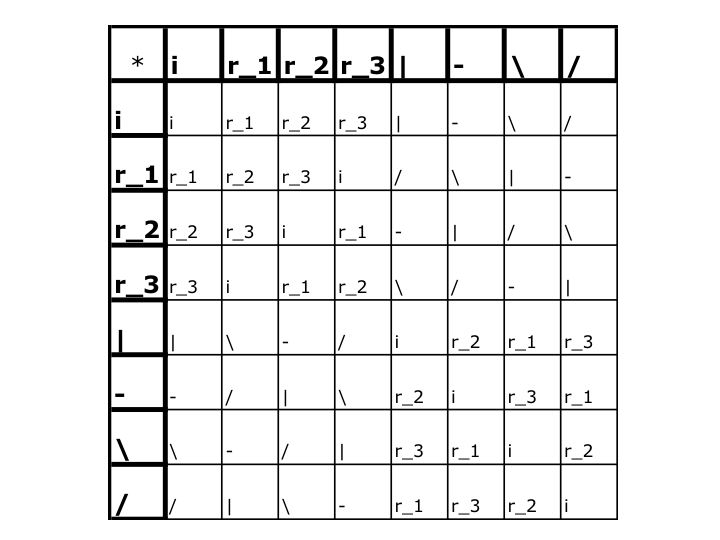
There are 4 reflections: horizontal, vertical, /, and \. So we get 4 elements out of the reflectional symmetries.

Using the origin, we can rotate a square counterclockwise 90 degrees, 180 degrees, and 270 degrees so this produces 3 elements in the symmetry group of a square.

Lastly, we have the identity.

Using the chart above we can determine that the symmetries of a square do in fact form a group.

So there are 8 elements in the symmetry group of a square.

Subgroups

S = {r_1, r_2, r_3, i}, G = {\, i}, H = {-, i}, I = {/, i}, J = {|, i}

[TOP]

Elements in the Symmetry Group of a Tetrahedron

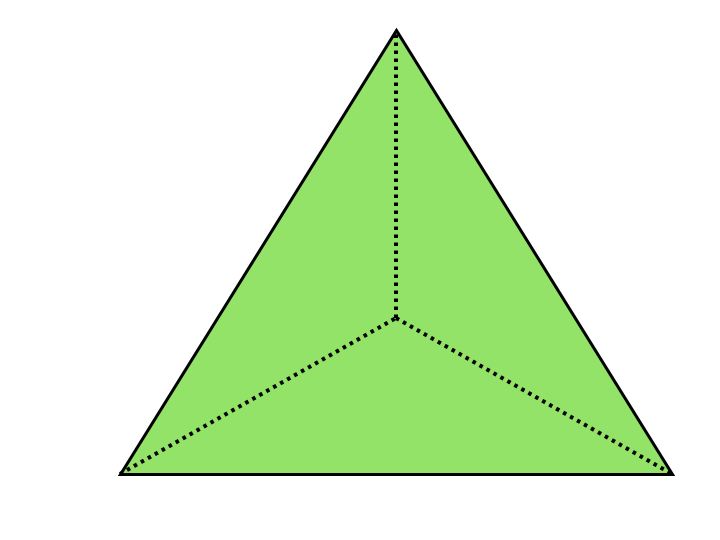
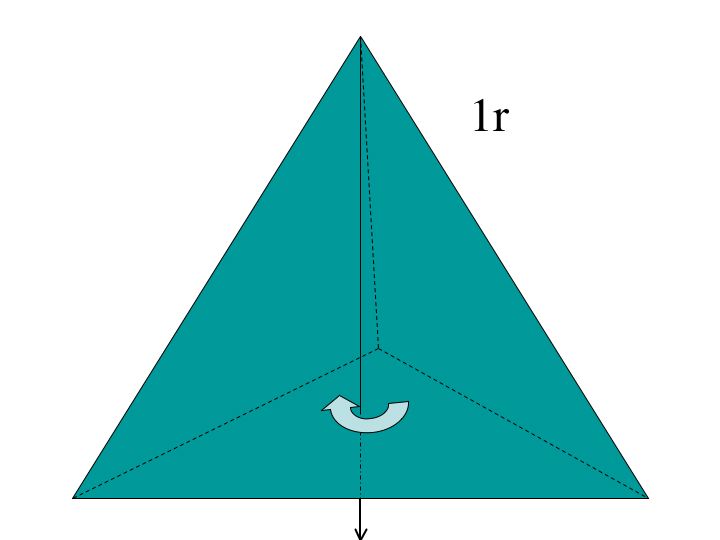
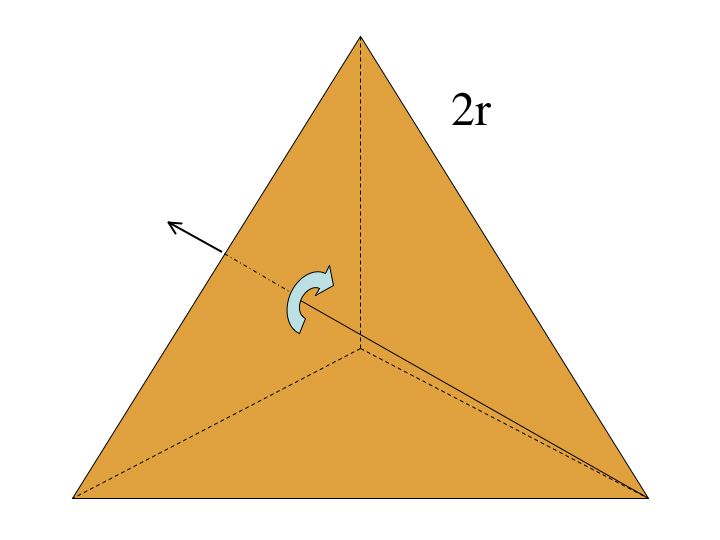
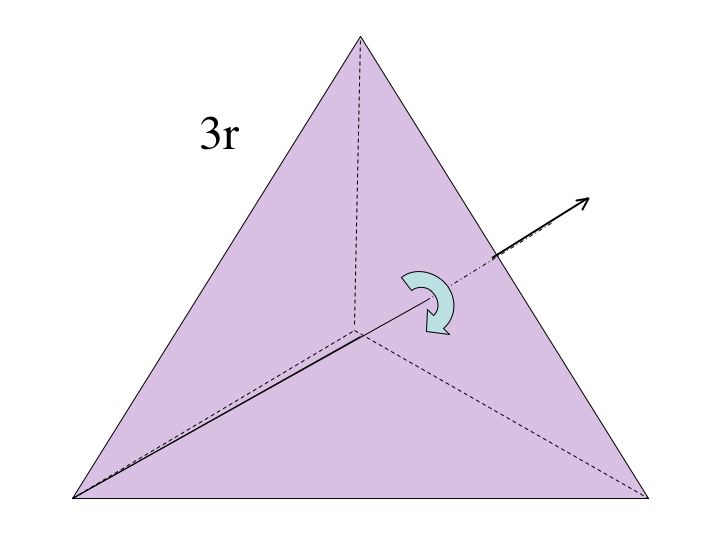
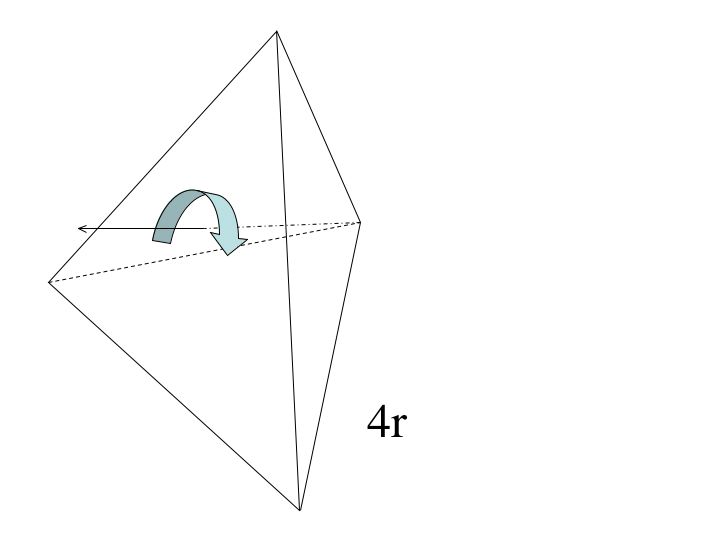
There are 12 elements in the symmetry group of a tetrahedron. We obtain 8 of these elements through rotating the preimage, 3 from reflecting it, and finally the identity.

There are 4 corners to a tetrahedron. The rotational symmetries can be found by drawing a line fron a corner through the oriding of the opposite side (or face). Now rotate clockwise by 120 degrees (I call this r_1). Rotate it another 120 degrees and we get what I call r_2. Finall if we rotate the tetrahedron another 120 degrees we get back to the preimage. Since there are a total of 4 corners, we get 8 elements.

Since there are 6 edges, we obtain 3 elements by reflecting about a line connecting the midpoint of one edge to the midpoint of its opposite edge. Using the figure below I labled 1s as the line connecting a to b. 2s as the line connecting c to d and 3s as the line connecting e to f.

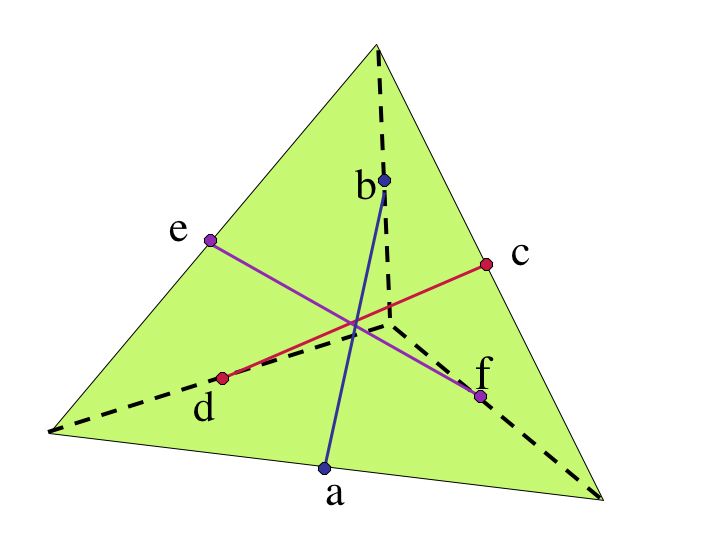
Subgroups

How many subgroups exist within the symmetry group of a Tetrahedron? I will leave that up to you, the reader to think about.

[TOP]

Elements in the Symmetry Group of a Cube

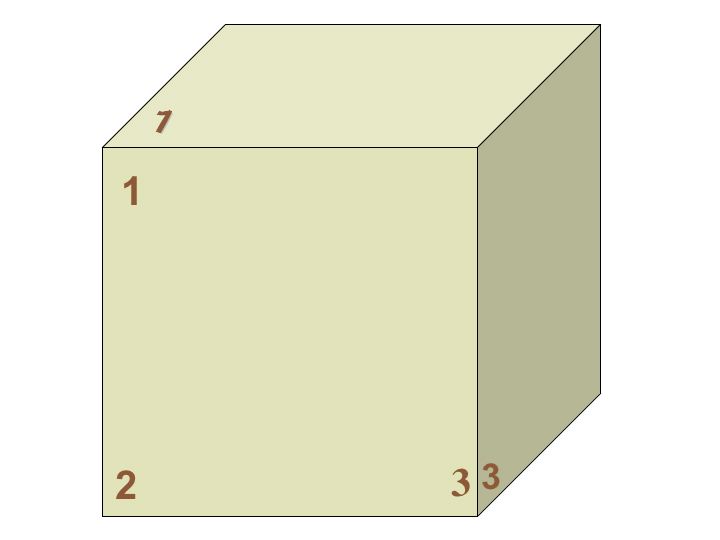
There are 8 corners of a cube. Let's label the corners. We can pick any corner as 1. After we have chosen corner 1, there are 3 possible corners that we can label as 2. Once 1 and 2 are in place, there are 2 only corners that could be corner 3. Once we have labeled corner 1,2, and 3 we are done since given a cube with three corners labeled we have enough information to label the rest.

Therefore, 8 x 3 x 2 = 48, so there are 48 elements in the symmetry group of a cube.

1 element is the identity, 23 elements come from rotating the primage, and the other 24 come from reflecting the preimage. When we reflect the preimage we must turn the image inside out. In order to do this we must go into the fourth dimension. We can however rotate the preimage in the third dimension.

There is no table for the elements of a cube. Why is this? Frankly, this is a large set, and so it is more difficult to put it into table form and once in table form it would be difficult to use.

Much like the group of symmetries of a triangle and that of a square, we can form a subgroup of the rotations plus the identity. It happens that these 24 elements are those elements that we can see in the third dimension since when we rotate a three dimensional object in real life, such as a book, we can see the object as it moves. In linear algebra terminology, we consider linear transformations with determinate 1 those that take the cube to itself and linear transformations with determinate -1 those that invert the cube and require 4-dimensions in which to do so.

[TOP]