Fields

[Definitions] [Example]

Definitions

Field:

In order to define a field, we first need some background about rings:

Ring

A ring is an algebraic system with two operations. A nonemty set R is considered a ring if in R there are two operations, + and · such that:

a) closure: a,b in R implies a + b in R and a · b in R

b) commutativity: a + b = b + a for a,b in R

c) associativity: (a + b) + c = a + (b + c) and (a · b) · c = a · (b · c) for a,b,c in R

d) identity: There exists 0 in R s.t. a + 0 = a for every a in R

e) additive inverse: Given a in R there exists a,b in R s.t. a + b = 0

f) distributive laws: a · (b + c) = a · b + a · c and (b+c) · a = b · a + c · a for a,b,c in R

Commutativity

A ring is commutative if a · b = b · a and a + b = b + a

Division Ring

A ring R with unit is said to be a division ring if for every a 0 in R there is an element b in R such that a · a^(-1) = a^(-1)· a = 1

Field

A ring R is said to be a field if R is a commutative division ring.

[TOP]

Is this set a Field?

Let's look at the set {0,1,2,3,4,5} mod 6.

Closure under multiplication

0 mod 6 · a mod6 0 mod6 where a is in the set {0,1,2,3,4,5}

1 mod 6 · a mod 6 a mod 6 where a is in the set {0,1,2,3,4,5}

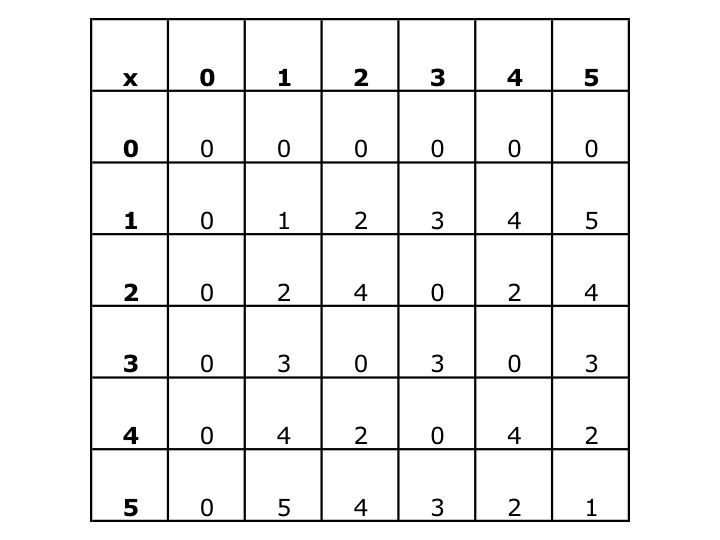
Using the chart below, we can show that there is closure under multiplication.

The chart below shows that the set is closed under addition.

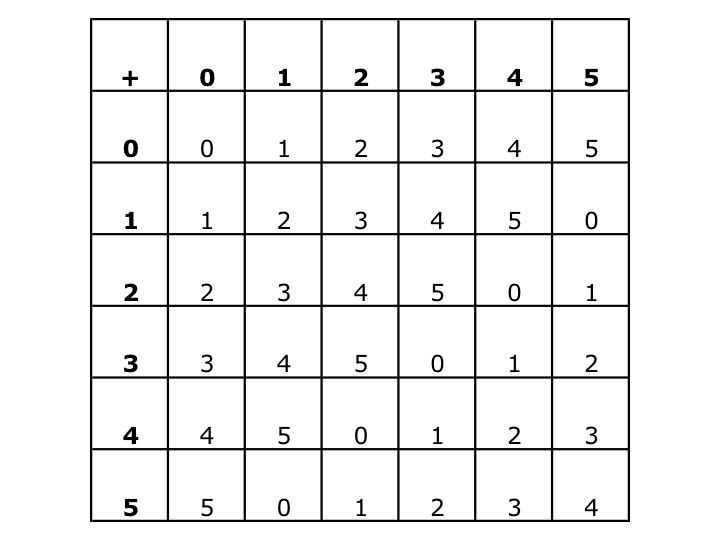
From the two charts we can see that the communitivity prperty holds and with the added bonus of a some tedious work, we can show that the associative property holds.

The identity under addition is 0. 1 and 5 are inverses of each other, 2 and 4 are inverses of each other, and 3 is its own inverse.

Distributive Law

a · (b + c) = a · b + a · c holds true

Remembering that b + c is less than 6. Let a be in the set {0,1,2,3,4,5}.

a· (0) = 0 = (a· 0 + a · 0) (mod 6)

a · (1) = a = (a · 0 + a · 1) (mod 6)

a · (2) = 2a = a · 1 + a · 1 = (a · 0 + a · 2) (mod 6)

a · (3) = 3a = a · 0 + a · 3 = (a · 1 + a · 2) (mod 6)

a · (4) = 4a = a · 0 + a · 4 = a · 1 + a · 3 = (a · 2 + a · 2) (mod 6)

a · (5) = 5a = a · 0 + a · 5 = a · 1 + a · 4 = (a · 2 + a · 3) (mod 6)

These are just a few of the possibilities. There are an infinite number of possible integers that are equivalent to a mod 6 where a is in the set {0,1,2,3,4,5}. For instance, a · 1 = a = a · 7 = (a · 3 + a ·4) (mod 6). After some consideration we can make the assumption that the distributive laws hold true.

Therefore the set is a ring. The last thing we need to check before we can call this ring a field is whether it is a division ring, a · a^(-1) = 1. However this property does not hold because there does not exist an element that can be multiplied to 2 to equal 1 nor does there exist an element for 3 or 4.

So the set {0,1,2,3,4,5} mod 6 does not form a field.

Alteration

However if we alter this set, to the set of integers mod p where p is prime, then the set will form a field. The properties we found in the set earlier still hold for this set. So for now we know we have a commutative ring with a unit. By Fermat's theorem, a^(p-1) 1 mod p. Given a in the set, its inverse is a^(p-2), since a · a^(p-2) 1 mod p. Therefore every element has an inverse, so the set is a commutative dividision ring and thus a field.

[TOP]