Polynomials

[Definitions] [Properties] [Examples] [Graphing] [Factoring] [Solving Equations]

Definitions

Definition of Polynomial in x

A polynomial in x is an expression of the form (a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0.

Degree

Given a polynomial (a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0, if a_n =/ 0, then the polynomial is of degree n.

Leading Coefficient

Given a nonzero a_n in (a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0, a_n is called the leading coefficient of the polynomial.

Standard Form

A polynomial is in standard form if it is written in descending powers of x.

Monomial

Polynomials with one term

Binomial

Polynomials with two terms.

[TOP]

Properties

Adding Polynomials

((a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0) + ((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) = ((a_n) + (b_n))x^n + ... + ((a_2) + (b_2))x^2 + ((a_1) + (b_1))x + ((a_0) + (b_0))

Subtracting Polynomials

((a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0) - ((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) = ((a_n) - (b_n))x^n + ... + ((a_2) - (b_2))x^2 + ((a_1) - (b_1))x + ((a_0) - (b_0))

Multiplying Polynomials

When multiplying two polynomials, we use the distributive property to multiply each term in one polynomial with each polynomial in the other polynomial. Often times when we are multiplying two binomials, we refer to this as the foil pattern.

FOIL = Product of first terms + product of outer terms + product of inner terms + product of last terms

((a_1)x + (a_0))((b_1)x + b_0) = (a_1)(b_1)x^2 + (a_1)(b_0)x + (a_0)(b_1)x + (a_0)(b_0)

In general, when multiplying two polynomials, make sure to multiply every term in one polynomial with each term in the other polynomial. This comes from the distributive property that says x(y + z) = xy + xz. If you are multiplying two polynomials, you need to make sure to distribute each term.

((a_n)x^n + ... + (a_2)x^2 + (a_1)x + a_0) · ((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) = (a_n)x^n((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) + (a_(n-1))x^(n-1)((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) + ... + (a_2)x^2((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) + (a_1)x((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) + a_0((b_n)x^n + ... + (b_2)x^2 + (b_1)x + b_0) = (a_n)(b_n)x^2n + ... + ((a_2)(b_0) + (a_1)(b_1) + (a_0)(b_2))x^2 + ((a_1)(b_0) + (a_0)(b_1))x + (a_0)(b_0)

Special Product Patterns

Sum and Difference:

(u + v)(u - v) = u^2 - v^2

Square of a Binomial:

(u +v)^2 = u^2 +2uv + v^2

(u-v)^2 = u^2 -2uv + v^2

Cube of a Binomial:

(u + v)^3 = u^3 + 3u^2v +3uv^2 + v^3

(u-v)^3 = u^3 - 3u^2v - 3uv^2 - v^3

Dividing Polynomials

Synthetic Division

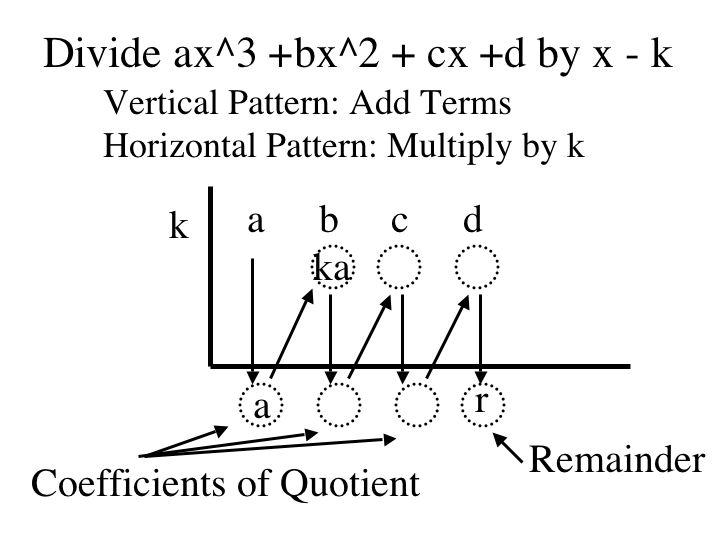
Long Division

[TOP]

Examples

Adding Polynomials

(2x^4 + 3x^2 +2x + 10) + (8x^3 + 15x^2 + 91x + 7) = 2x^4 + 8x^3 + 18x^2 + 93x + 17

(-27x^2 + 15x - 84) + (13x^3 + 27x^2 - 3x + 72) = 13x^3 + 12x - 12

Subtracting Polynomials

(3x^2 + 7x + 10) - (x^2 + 4x + 9) = 2x^2 + 3x + 1

(4x^4 + 19x^2 - 17x + 2) - (5x^4 + x^3 - 12x^2 - 5x + 6) = -1x^4 - x^3 + 31x^2 - 5x - 4

Multiplying a Monomial and a Trinomial

4x(3x^2 + 2x -5) = 12x^3 8x^2 -20x

Multiplying Two Binomials

(3x +2)(2x-7) = 6x^2 -21x +4x - 14 = 6x^2 - 17x - 14

Multiplying Two Polynomials

(3x^2 + 2x -4)(8x + 1) = 24x^3 + 3x^2 + 16x^2 + 2x - 32x - 4 = 24x^3 + 19x^2 - 30x - 4

Finding the volume of a Box

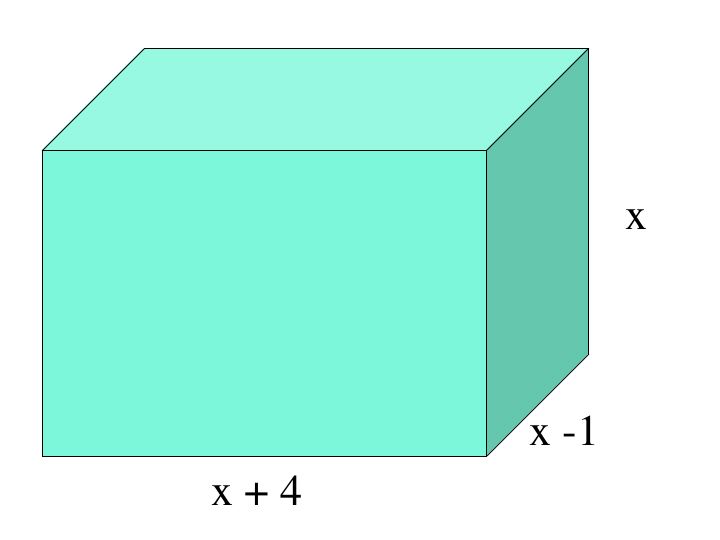
(x+4)(x-1)(x) = (x^2 +3x -4)(x) = x^3 + 3x^2 -4x

Long Division of Polynomials

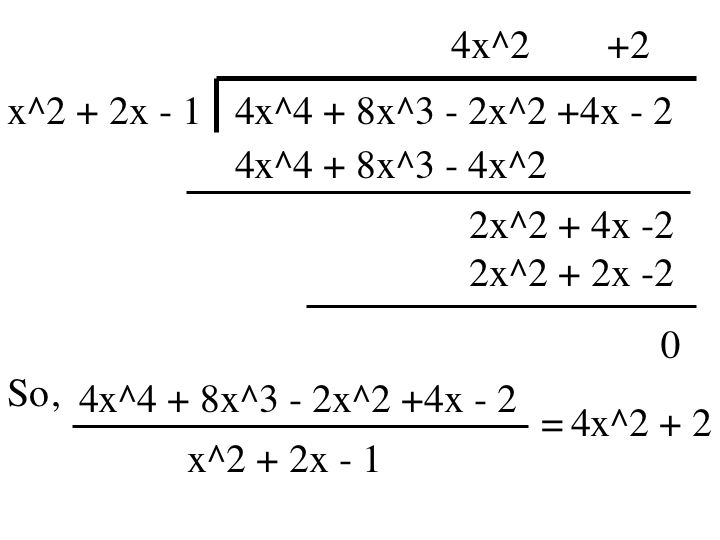
Synthetic Division of Polynomials

[TOP]

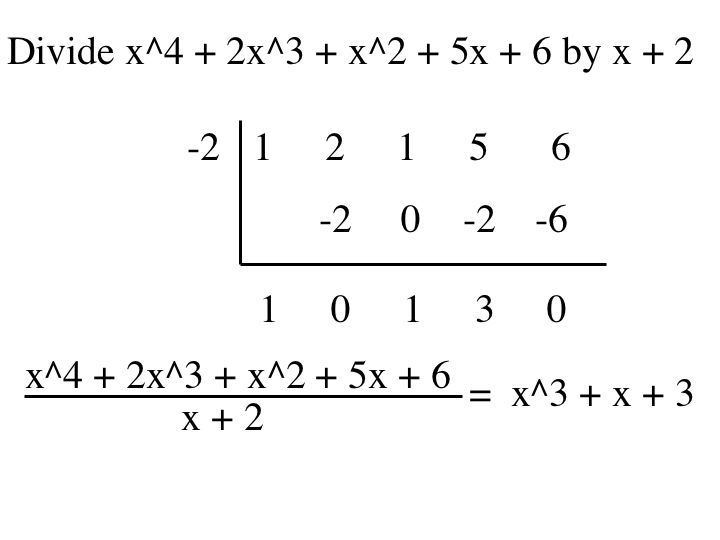
Graphing a Polynomial Function

A function of the form f(x) = (a_0)x^n + (a_(n-1))x^(n-1) + ... + (a_1)x + a_0, a_n =/ 0 is a polynomial function of degree n.

The graph of a polynomial function is continuous.

If the leading coefficient of the polynomial function whose degree is greater or equal to two is positive then the slope will be positive. If the leading coefficient of a polynomial of a degree greater than or equal to two is negative then the slope will be negative.

A monomial function, f(x) = a has degree 0 will graph as a horizontal line.

A binomial function, f(x) = ax + b of degree 1 will be a line with slope a.

A trinomial function, f(x) = ax^2 + bx + c, of degree 2 is a parabola.

[TOP]

Factoring Polynomials

When factoring polynomials, we always factor into degree 2 or or smaller.

Factoring out a monomial: (ax^2 + bx) = x(ax + b)

Example: 3x^2 + 6x = 3x(x + 2)

Finding the difference of squares: (a^2)x^2 - b^2 = (ax - b)(ax + b)

Example: 4x^2 - 36 = (2x - 6)(2x + 6)

Factoring a perfect square trinomial: x^2 - 2ax + a^2 = (x - a)^2

Example: x^2 - 10 + 25 = (x - 5)^2

Factoring a trinomial: ax^2 + bx + c = (gx + d)(fx + e) where c = de, a = gf, b = ae - df

Example: 6x^2 + 11x - 35 = (3x - 5)(2x + 7)

Factoring by grouping: ax^3 - abx^2 - x + b = ax^2(x - b) - (x - b) = (ax^2 - 1)(x - b)

Example: 4x^3 - 2x^2 - 6x + 3 = 2x^2(2x - 1) - 3(2x -1) = (2x^2 - 3)(2x - 1)

Factoring the sum of two cubes: u^3 + v^3 = (u + v)(u^2 - uv + v^2)

Example: 8x^3 + 27 = (2x + 3)(4x^2 - 6x + 9)

Factoring the difference of two cubes: u^3 - v^3 = (u - v)(u^2 + uv + v^2)

Example: 125x^3 - 64x^3 = (5x - 4)(25x^2 + 20x + 16)

[TOP]

Solving Polynomial Equations

Zero Product Property: Let a and b be real numbers. If ab = 0 then a = 0 and b = 0.

Take an equation

Step 1: Collect all terms on one side

Step 2: Factor out the terms

Step 3: use the zero product property to solve for each x.

The power of the polynomial determines the maximum number of solutions.

Example: 24x^3 = 40x^2 - 16x

24x^3 + - 40x^2 - 16x = 0

4x(6x^2 - 10x - 4) = 0

4x(3x + 1)(2x - 4) = 0

4x = 0 & 3x + 1 = 0 & 2x -4 = 0

So, x = 0, x = -1/3 & x = 2 by the zero product property.

[TOP]