Fibonacci Mobile
The mobile pictured below, designed and constructed by Alison Frane and Susan Goldstine, hangs by the entrance of the Mathematics and Computer Science Department of St. Mary's College of Maryland. The hanging elements are made of watercolor paper that is painted in our school colors, blue on one side, gold on the other.
 |
|
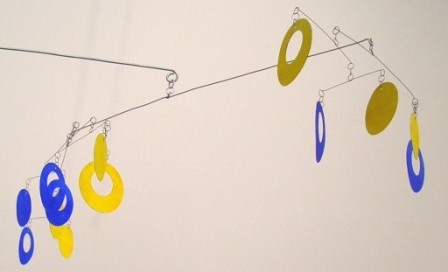
An Eight-Element Bar |
|
 |
|
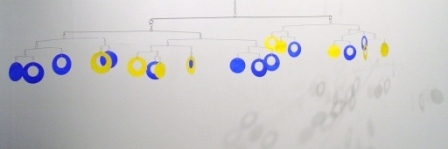
A Thirteen-Element Bar |
|
 |
|
 |
|
 |
|
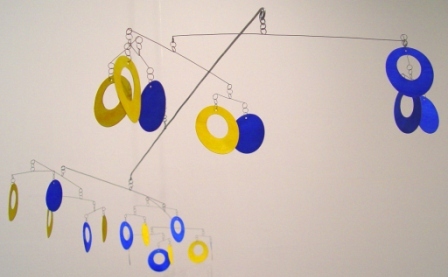
The Full Mobile |
|
|
| |
The Full Mobile, Mobile |
As in the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34,..., where each number is the sum of the previous two numbers, in this mobile each bar is the sum of the previous two bars.
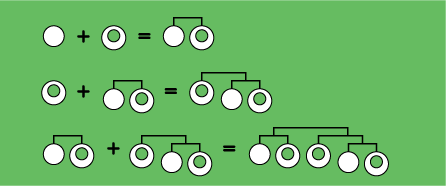 |
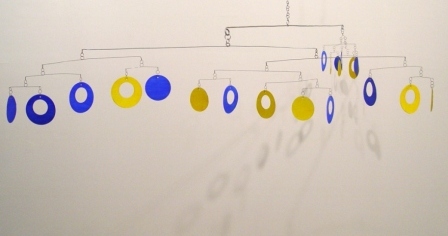
The mobile contains a total of 21 hanging elements, of which 13 are loops and 8 are disks. There are eight 2-element bars, five 3-element bars, three 5-element bars, two 8-element bars, one 13-element bar, and one 21-element bar, which supports the entire mobile.
For optimal spacing of the mobile, the length of each bar is the golden ratio times the length of the previous bar. The golden ratio is (not coincidentally) the limiting value 1.61803... of the sequence 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21,... of ratios of consecutive Fibonacci numbers.
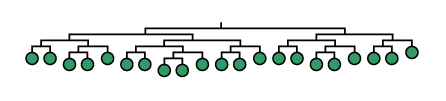 |
Schematic of the Full Mobile |
Each bar balances two consecutive Fibonacci numbers of hanging elements. For example, a five-element bar has two elements (a disk and a loop) hanging from one end and three elements (a disk and two loops) hanging from the other. The paper is cut so that the disks and loops have exactly the same weight. This means that if we assume that the weight of the wires has a negligible effect on the position of the balance points (and surprisingly, this is empirically the case), the balance points will divide each bar into one of the Fibonacci ratios above. The larger the mobile, the closer the final balancing point gets to dividing the top bar into the golden ratio.
The master mobile maker Alexander Calder used the Fibonacci pattern in a closely related but different way in his 1957 sculpture Black, White, and Ten Red, which is in the collection of the National Gallery of Art in Washington, D.C. Calder's mobile contains a total of twelve hanging elements, where
12 = 1 + 1 + 2 + 3 + 5
 |
Susan and Alison with
|