Presentation Notes
(NOT PART OF THE SLIDES)
The first time I
saw this proof of the Brouwer Fixed Point Theorem was in a talk by Francis Su
in Trivial Notions, the graduate student seminar in the Harvard math
program. For this reason, I have opened
the talk with a plug for Francis’s Math Fun Facts, which is a
wonderful source of mathematical gems for students and teachers alike. While the site does not contain the proof
given below, as it is too long to fit the site’s mandate, there are Fun Facts
on Sperner’s Lemma and on the crumpled paper
problem.
This talk begins
with a demonstration. I show a piece of
regular 8.5x11 paper and mark its position on a
tabletop. I ask a randomly chosen member
of the audience to crumple the sheet of paper, taking care not to rip it in the
process. Another member of the audience
is enlisted to place the paper inside the marks on the tabletop.
I then present
the audience with the following wager: I
bet that there is a point on the page that lies directly above its former
position. The audience votes on my odds
of winning: 50%, 75%, 90%, 100%. People who have not seen this illustration or
the theorem will usually lower their hands before I reach 100%.
At this point, I
get someone in the audience (a prearranged plant) to actually take the
bet. For the rest of the talk, I am
arguing that I get to keep the money.
This is where the slides start.
This talk is brought to you
by
Francis Su’s Math Fun Facts.

The Brouwer Fixed Point Theorem
If f: D→D is a continuous function, then there
is a point a in D such that f(a) = a.
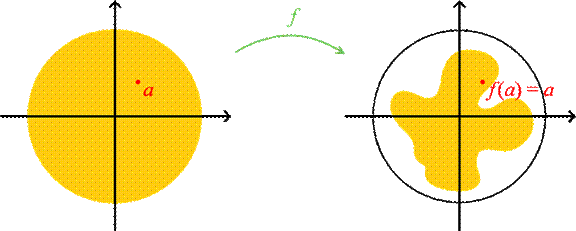
Definition: D = {(x,y) : x2
+ y2 ≤ 1}
D is the
closed unit disk.
Continuity in
R:
Definition: A function f: R→R is continuous
at x if for every ε > 0, there is a δ > 0 such that
if |x – x′| ≤ δ,
then |f(x) – f(x′)| ≤ ε.
The Brouwer Fixed Point Theorem:
If f: D→D is a continuous function, then there
is a point x in D such that f(x) = x.
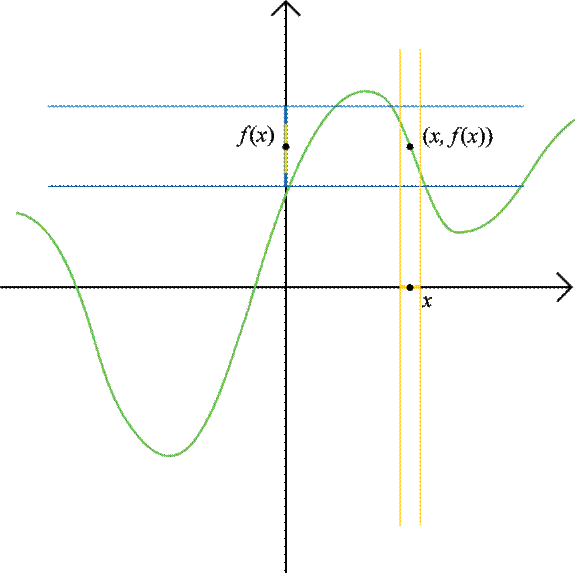
Continuity in
R2:
Definition: A function f: R2→R2 is continuous at x
if for every ε > 0, there is a δ > 0 such that
if |x – x′| ≤ δ,
then |f(x) – f(x′)| ≤ ε.

Intuition:
The plane is made of infinitely stretchable, infinitely compressible
material. f rearranges the plane without tearing it.
The One-Dimensional BFPT
If f:[0,1]→[0,1] is a continuous function, then it has a fixed
point.
Proof: Look at the function g(x) = f(x)
– x.
g(0) = f(0) ≥ 0
g(1) = f(1) – 1 ≤ 0
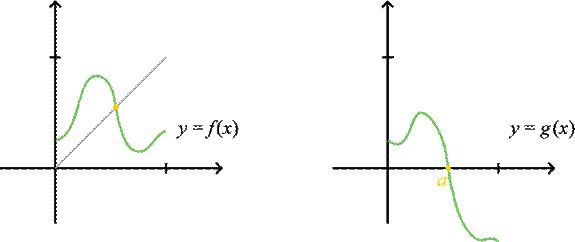
By the Intermediate Value
Theorem, somewhere between 0 and 1 is an a such that g(a)
= 0. Thus f(a)
= a.
Presentation Notes
When I present
the one-dimensional Brouwer Fixed Point Theorem, a common calculus exercise, I
mention that there is also an n-dimensional
version of the theorem. The proof
presented here works in n dimensions,
and I challenge the more ambitious audience members to figure out how to extend
the argument to higher dimensions.
I also point out that while the proof above will not work in two
dimensions, since there is no analogue of the Intermediate Value
Theorem for functions on the plane, our proof will use a similar
technique for building a function that compares
f
(x) to
x.
In the next
slide, we consider the essential properties of D by looking at sets which admit continuous maps with no fixed
points. We begin by observing that the
shape of D had better not be one of
these properties if I want to apply the theorem to a rectangular piece of
paper.
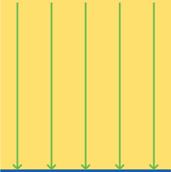
Food for Thought: What’s special about D?
1.
D is
bounded.
2.
D is closed.
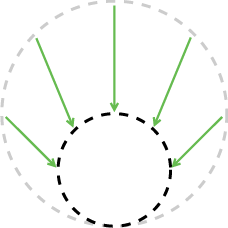
3.
D is
connected.
Exercise:
What property is missing?
Definition: If S
is a set in R2 and R is a subset of S, a retraction of S onto R is a
continuous function g: S→R such that every point of R
is fixed.
Example:
S
= the square {(a,b) : a,b
are in [0,1]}
R
= the bottom edge {(a,0) : a is in [0,1]}
g(x,y) = (x,0) is a
retraction from S
to R.
Let C = {(a,b) : a2 + b2 = 1}
=
the boundary of D.
The No Retractions Theorem (NRT)
There is no retraction from D onto C.
STEP 1.
Claim: BFPT
is true ↔ NRT is true.
Equivalently, BFPT is false ↔
NRT is false.
Proof: (→)
Suppose BPFT is false, and let
f: D→D be a continuous function with no fixed points. We form a retraction g: D→C as follows.
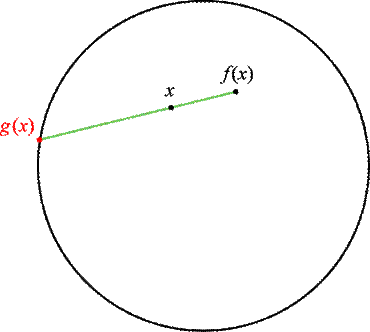
g is continuous and g fixes each point of C.
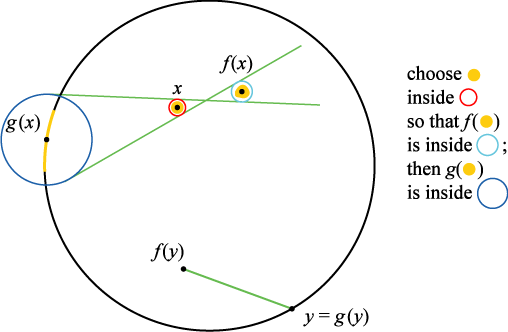
So NRT is false.
(←)
Suppose NRT is false, and let
g: D→C be a
retraction. Then
f(x,y) = –g(x,y)
(retract and then rotate) is
continuous and has no fixed points.
So BFPT is false.
Presentation Notes
As soon as I
begin the actual proof of the Brouwer Fixed Point Theorem, I make it clear that
this will be a proof in four steps. Now,
at the end of the first step, I note that the audience may be less than
satisfied with our progress. After all,
we have just taken one theorem that we don’t know how to prove and shown that
it is equivalent to another theorem that we don’t know how to prove.
Nonetheless, I
claim that we have gained something. The
Brouwer Fixed Point Theorem is far from obvious—a point that I can reinforce by
the observation that some of them bet against it—while the No Retractions
Theorem is utterly self-evident.
To illustrate
this, I use a cylinder (most recently, an oatmeal container) with a piece of a
balloon stretched over it to represent the disk D. After prying at it for a
while in a vain attempt to retract it onto its boundary, I comment that the
only way that we can achieve the map is by doing “this,” at which point I pop
the balloon. The noise is very
satisfying.
I usually observe
that the No Retractions Theorem is so intuitively obvious that perhaps my
opponent will consider forfeiting the bet now.
Needless to say, this does not happen.
The rest of the
proof involves assuming that we have a retraction of a disk (eventually, a
triangle) onto its boundary and finding the tear that we know must be there.
At Step 2,
on the next slide, I fill in the sample triangulation with a Sperner
labeling as I define the concept. The rules for such a labeling
are that the vertices of the big triangle are labeled A, B, and C,
the vertices along an outer edge may only be labeled by the two
letters at the edge's endpoints, and the middle vertices may be
labeled with any of the letters A, B, and C.
I allow the audience to call out
some of the letters as we go.
At Step 3, when
the technique for changing shape is described, I point out that the same
technique allows me to apply the Brouwer Fixed Point Theorem to a rectangular
region.
STEP 2.
Sperner’s Lemma: Locating the tear.
Start with a triangle, and
triangulate it.
A Sperner
labeling:

Sperner’s
Lemma: Any Sperner labeling contains
an ABC triangle.
Proof:
Along the outer edge from
vertex A to vertex B, there is an odd number of AB edges.
![]()
Score the labeling as
follows:
1 point for every external AB
edge
2 points for every internal AB
edge
The total score is odd.
We get the same score by
giving each triangle 1 point for every AB edge
it contains.

Since the total score is odd,
there is an odd number of ABC triangles, and hence at least one.
STEP 3.
Changing shapes.
Let T be a closed triangular region in R2.
We can define a map σ: T→D by:
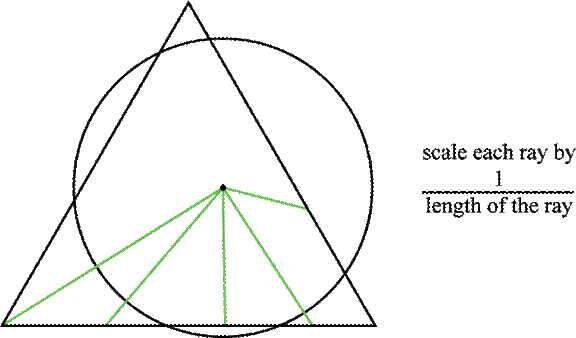
σ is a continuous
one-to-one correspondence between T
and D which sends the boundary of T to the boundary of D.
If g is a retraction from D
to its boundary,
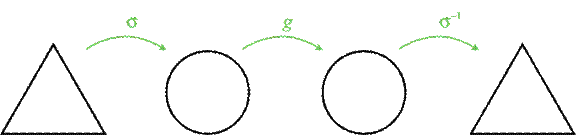
then σ−1°
g ° σ is a retraction
from T to its boundary.
Thus, to prove NRT, it
suffices to show that there is no retraction from T to its boundary.
Interlude.
We need the following.
Definition: f: S→S is uniformly
continuous on S if for every ε > 0, there is a δ > 0 such
that for
every x in S,
if |x – x′| ≤ δ,
then |f(x) – f(x′)| ≤ ε.
Intuition:
There is an upper bound to the stretchiness of f.
Example: f(x)
= 1/x is not uniformly continuous on
(0, 2).
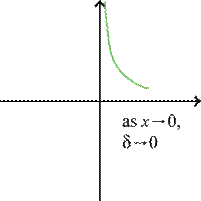
BUT if S is closed and bounded (like D
and T), then any continuous
function on S is uniformly
continuous.
Advanced Calculus, Gerald B. Folland, pp. 39-40.
STEP 4.
Proof of NRT:
Suppose g were a retraction from T
to its boundary.
Pick a very small ε, and
choose a corresponding δ. Now,
triangulate T with triangles whose
sides are smaller than δ.
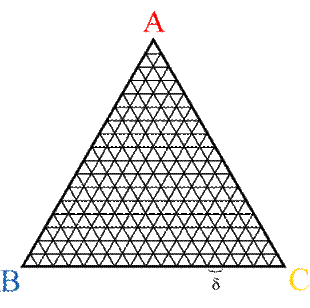
Label the vertices of T by A, B, and C, and
label each vertex v in the
triangulation by which of A, B, or C is
closest to g(v).
Since g fixes the boundary of T,
this is a Sperner labeling. By Sperner’s Lemma, we have an ABC triangle,
whose vertices we will call x, y, and z.

But x, y, and z are within δ of each
other, and g(x), g(y), and
g(z) are
farther apart than ε.
CONTRADICTION.
Therefore, NRT is true.
Therefore, BFPT is true.