Sample Abstract
Most decorative patterns in knitting, embroidery, weaving, and other fiber arts employ symmetry. Or, to be more precise, they employ symmetries, and mathematically-minded devotees of these art forms are interested in the variety of different symmetries accessible in each medium.

In this talk, we will explore the mathematical theory of symmetry and its application to traditional and contemporary fiber arts. No special background in math or fiber arts is required, and there are myriad ideas and images here for both novices and experienced practitioners of mathematics and of knitting.

Alternate Title
Symmetric Threads: Classifying Symmetries in the Fiber Arts

Level
General/Advanced High School and up.

In principle, the primary form of this talk is suitable for a general audience, as it is driven by mathematical artworks and hence packed with pretty pictures. However, it will resonate best with an audience that has the mathematical instincts and focus to search for geometric patterns in the various photographs and diagrams. With an advanced undergraduate audience, we can delve more deeply into the underlying group theory.

Alternately, I can center the art and de-emphasize the math, but I am less inspired to travel a significant distance for this version unless the venue has a particular connection to fiber arts.

Mechanics
For this talk, I need a computer projector. I also exhibit and pass out models, so the room needs not to be too dark.

Sample Abstract
Sometimes, when opportunity knocks, it comes bearing jewelry.

Many years ago, I embarked on an unexpected journey into the realm of mathematical beading. Along the way, my colleagues and I uncovered fascinating connections between mathematics and art, and I will show you a few of the highlights of our travels into the realms of geometry, number theory, topology, and abstract algebra. Together, we will look at how geometry and modular arithmetic intersect in bead crochet, the structure of symmetry, the aesthetic principles of jewelry design, and bracelets. Lots and lots of bracelets.

No special mathematics background is needed for this talk.

Level
High School and up.

The level of this talk is adaptable, but I usually pitch it to undergraduates or enthusiastic younger students. Any audience who is open to looking for numerical patterns and playing with geometric intuition can appreciate the mathematical content in this general version. With an advanced undergraduate audience, we can delve into some abstract algebra and topology.

Mechanics
For this talk, I need a computer projector. I also exhibit and pass out models, so the room needs not to be too dark.

Sample Abstract
‘You have heard of Fortunatus's Purse, Miladi? Ah, so! Would you be surprised to hear that, with three of these leetle handkerchiefs, you shall make the Purse of Fortunatus, quite soon, quite easily?’

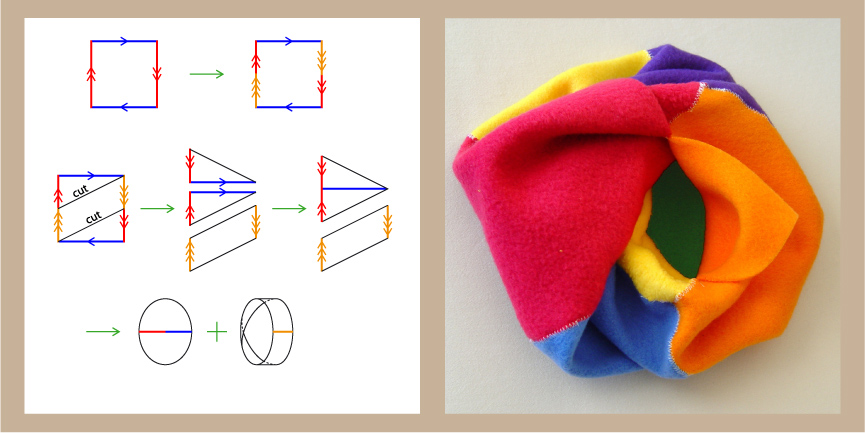
In the mathematical wonderland of topology, we can hold the entire world in a bottle or in a purse. We will assemble this purse, dissect it, rearrange it, and see what it has to tell us about how our world fits together.

Alternate Titles
Fortunatus’s Purse and the Wealth of the World
Fortunatus’s Purse: a many-colored story

Level
Advanced High School and up.

The talk uses some topological gluing diagrams and a little geometry in three-space, all of which are carefully explained during the talk, but this might be a stretch for an early high school audience. An undergraduate audience should follow all of the material and will find lots of fascinating new ideas.

Mechanics
For this talk, I need a computer projector and a speaker system to play a short but essential audio file. I also exhibit and pass out models, so the room needs not to be too dark.

Sample Abstract
A recurrent theme in the intoxicating images of M.C. Escher is the division of the plane into animal figures. Underlying each division is a tiling of the plane by simple polygons. Escher's spirit of artistic adventure led him to explore more exotic patterns, and we will follow his path into tilings of the sphere and of the hyperbolic plane.

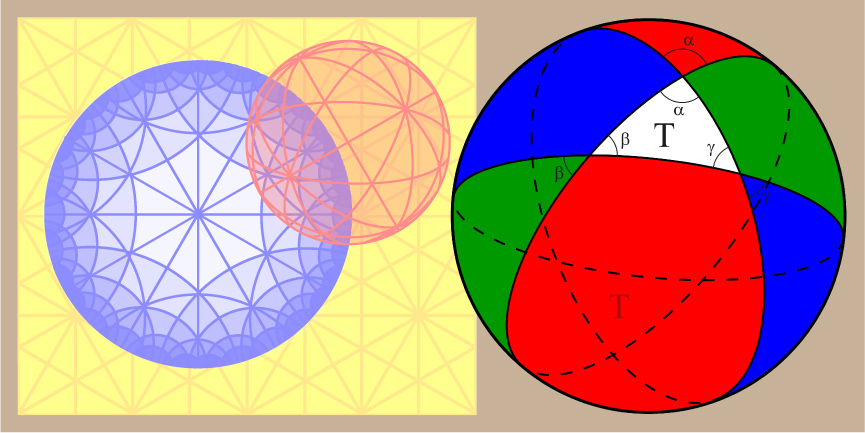
If you know that the sum of the angles in a triangle is 180 degrees, then you can follow the math in this talk.

Level
High School and up.

The claim in the abstract that it is sufficient to know the angle sum in a Euclidean triangle is accurate. At some points in the talk I do use radians instead of degrees, but not in a way that involves any higher math.

Of course, the claim is also ironic, since the talk includes non-Euclidean triangles, whose angle sum is not 180 degrees.

Mechanics
For this talk, I need a computer projector. I also exhibit and pass out models, so the room needs not to be too dark.