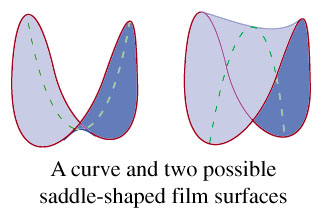In 1829, the Belgian professor of Physics and Anatomy Joseph Plateau permanently damaged his eyes in an optical experiment that involved staring at the sun for twenty-five seconds. At the same time, he became interested in the physical and geometrical properties of soap film surfaces, which are elastic in the sense that they have the smallest possible area. Despite being completely blind by 1843, Plateau continued his research with help from his family and fellow scientists, and published many papers on the subject. Meanwhile, a mathematical theory of surfaces that minimize their area had begun over the course of the previous century, when the mathematicians Bernoulli, Euler, and Lagrange developed the "Calculus of Variations." A mathematical interest renewed by Plateau's experiments led to the formulation of the "Plateau Problems." For example, we may pose the following question: "Start with a circle of wire that has been twisted, bent, and stretched into some new shape. If we dip it into soapy water and pull it out again, what is the shape of the soap film that results?" Physically, surface tension makes the resulting soap film minimize its area while still spanning the wire frame. The analogous mathematical Plateau Problem is as follows: "You are given a bent circular curve in three dimensional space, like the wire figure. There are many different possible two-dimensional surfaces touching the entire given curve, like attached sheets of plastic wrap. Your task is to find the one that has the smallest total area." In the 1930s, Jesse Douglas and Tibor Radó finally showed mathematically that no matter what shape the curve has, there is always a least-area stretched disk spanning the curve. Further research, including work in the field of Geometric Measure Theory, showed that there is always a least area surface spanning the curve. Today research on various geometrical aspects of such surfaces continues across the country, often with the help of experimental equipment consisting of wire and soap water. For instance, in 1976 Jean Taylor proved that soap film surfaces can only intersect in two ways: three surfaces can intersect along a curve, meeting at equal angles of 120 degrees, or four surfaces can intersect at a point, meeting at about 109 degrees. This property was originally conjectured by Plateau himself.

 Before we can attempt to solve the Plateau Problem mathematically, we need precise definitions of concepts such as curve, surface, and area. The best definitions here would require a fair amount of calculus, and would lead us to some very interesting mathematical theories, including Einstein's relativity. Instead, let us consider some examples. Lines, circles, and the path traveled by a housefly are examples of curves. A circle is called a "closed curve" because a little person walking along it would return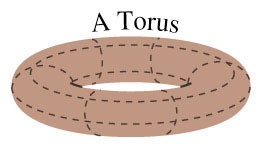 to the place she started. An important tool of calculus allows us to define a unique line that is tangent to a curve at any point. For example, a horizontal line is tangent to the top of a circle. Two-dimensional planes and spheres are examples of surfaces, as is a horse's saddle and a torus, which you can think of as the outer surface of a donut.  The sphere and torus are both examples of "closed surfaces," since they don't have boundary curves. At a point of a surface, there are lots of different lines that are tangent to the surface, but there can only be one tangent plane. For instance, a horizontal plane is tangent to the north pole of a sphere.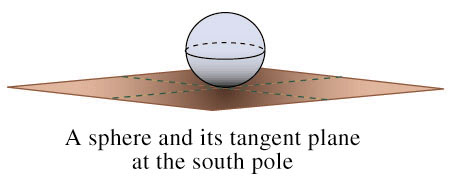

We may formulate a one-dimensional version of the Plateau problem as follows: "Given two points in space, find the curve connecting them which has the least distance. The solution, of course, is always a straight line segment." In attacking the two-dimensional problem, our intuition is that an area-minimizing surface should be as "flat" as possible, with no unnecessary hills or valleys. For instance, if we dip a perfectly circular wire into soapy water, the resulting soap film should be a flat disc spanning the circle. However, if our wire boundary is bent, then we expect that the surface with least area that spans it will have to bend some. The mathematical concept of curvature is a way to describe the bending of a surface.

 First, we can define this property for a curve by considering what happens to a tiny ant that walks along the curve with constant speed one centimeter per second. Its velocity, which tells us how fast it's going and in what direction, always points along the line tangent to the curve. We can imagine this as an arrow pointing out of the ant's head. The acceleration of the ant tells us how fast its velocity arrow is changing and in what direction. This arrow points in the direction the curve is bending, and is perpendicular to the tangent line. We call the ant's acceleration the "curvature vector" of the curve. For example, a line has zero curvature since its tangent line never changes, while a circle has a curvature of constant length pointing toward its center. To examine the geometry of a surface, we again place an ant and watch it move at constant speed.  But this time it can go in many different directions. So, there are many different kinds of curvature for surfaces. The most important one in the theory of soap films is the mean curvature, which is the average of the biggest (most positive) and smallest (most negative) curvatures of curves on the surface. Let us consider the example of a sphere, with the convention that the "up" direction from the surface points toward the center (we may think of an ant inside a round balloon). Then a point on the sphere will have a positive number for its mean curvature, because the surface curves upward in every direction. On the other hand, a saddle-shaped surface might have zero mean curvature where the rider sits, because in the minimal direction it curves downward (where the rider's legs might go), while in the maximal direction it curves upward (along the horse's spine). What do you think we can say about the mean curvature on a torus? An important mathematical theorem is this one: "If a two-dimensional surface spanning a boundary curve minimizes area compared to others spanning the same boundary, then this surface has zero mean curvature at every point." You can imagine for instance that if the surface had a mountain (with negative mean curvature), then a surface with the mountain cut off would have less area. The precise mathematical proof can be found in the references below. Notice that the implication here does not mean that every surface with zero mean curvature minimizes area. However, mathematicians call any surface with zero mean curvature a minimal surface.

There are many interesting and still unsolved problems in the theory of minimal surfaces. For example, one can find a curve in space which is the boundary curve of several different minimal surfaces. It is unknown whether there is a closed curve in space bounding an infinite number of minimal surfaces. A large amount of current research concerns the idea of minimal surfaces in higher dimensions. I have become interested in general geometric properties of higher dimensional minimal surfaces, such as how smooth or pointy they are.

 A slightly different unsolved problem involves soap bubbles rather than films. It is known that a spherical soap bubble is a surface that minimizes its area, subject to the restriction that it encloses a fixed volume. This mathematical fact was conjectured in ancient Greece. Now consider the problem of two bubbles. What is the best surface to enclose and sep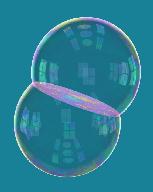arate two different volumes? By experimenting with bubbles, we can find a nice surface that should work, but how can we prove that it is the best? This question remained open until just recently, and it spurred much interesting research in an area known as Geometric Measure Theory. In 1996, a pair of mathematicians solved the case in which the two bubbles have equal volume, using a computer. In 1993, a group of undergraduate researchers succeeded in one lower dimension. That is, they showed that the standard double circle in the plane separating two regions of given area uniquely minimizes its perimeter. The three-dimensional problem was solved by Hutchings, Morgan, Ritore and Ros in 2000. The analogous problem for the triple bubble is wide open, and the two-dimensional version was the subject of a very recent PhD thesis.

Here is a practical version of the soap bubble problem that often appears in calculus classes: "A soup company wants to package its soup efficiently using cylindrical cans. The cans must be made to contain 16 cubic inches of volume. The top and bottom discs of the can cost fifteen cents per square inch to make, while the side costs twelve cents per square inch. What is the cheapest cylindrical can?"

References:

Colding, T. and Minicozzi, W, Minimal Surfaces. Courant Institute Lecture Notes 4, 1999.

Foisy, Alfaro, Brock, Hodges, and Zimba, "The Standard Soap Bubble in R2 Uniquely Minimizes Perimeter", Pacific Journal of Mathematics 159 (1993) p.47-59.

''Proof of the Double Bubble Conjecture'', by Michael Hutchings, Frank Morgan, Manuel Ritoré and Antonio Ros

Isenberg, Cyril, The science of soap films and soap bubbles. Tieto Ltd., Clevedon, 1978.

Morgan, Frank, Riemannian Geometry: a Beginner's Guide. Second edition. A K Peters, Wellesley, 1998.

Morgan, Frank, "Minimal Surfaces, Crystals, Shortest Networks, and Undergraduate Research", Mathematical Intelligencer 14 (1992) no. 3 p.37-44.

Morgan, Frank, "Mathematicians, Including Undergraduates, Look at Soap Bubbles", American Mathematical Monthly 101 (1994) no. 4 p.343-351.
(The problem of infinitely many minimal surfaces was addressed by a high school student in a letter to the author.)

Morgan, Frank, Geometric measure theory. A beginner's guide. Third edition. Academic Press, Inc., San Diego, CA, 2000.

Taylor, Jean E., "The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces". Annals of Mathematics (2) 103 (1976), no. 3, 489--539.

Internet Links:

• Minimal surfaces at Granada University with a list of galleries
• A brief biography of Joseph Plateau - and another one
• A Minimal Surface Library with pictures of lots of example surfaces
• Ken Brakke's formulation of minimal surfaces as minimum-area cuts separating multiple universes
• An article on a Westinghouse finalist from Gunn High School who worked on a soap-film problem
• A gallery of artistic representations of minimal surfaces from Matthias Weber at Indiana University
• The Brandeis University main catalogue of surfaces with 3D images
• Soap Bubble painting from the National Gallery of Art
• On the relation between soap bubbles and the distribution of luminous matter in the universe
• The GANG group at UMass with a nice gallery of surfaces

A Bubble Recipe:

Copyright: Alex Meadows, 2006